Question

4．如图，在△ABC中，∠ACB=90°，P为BC的中点，CD⊥AB于D，交AP于点F，PE⊥AP交AB于点E
（1）图中与△AFC相似的三角形为△PBE；
（2）如图1，当BC：AC=2时，求PF：PE的值；
（3）如图2，当BC：AC=n时，猜想PF：PE的值，并说明理由．

Answer 1

分析 （1）根据余角的性质得到∠ACD=∠B，∠CAF=∠BPE，根据相似三角形的判定定理即可得到结论；
（2）如图1，过P作PQ⊥BC交AB于Q，根据已知条件推出△ACP是等腰直角三角形，得到∠CAF=∠APC=45°，根据相似三角形的性质得到∠CAF=∠BPE=45°，∠AFC=∠BEP，求得∠EPQ=∠CPF=45°，∠CFP=∠PEQ，证得△PCF∽△PEQ，根据相似三角形的性质得到$\frac{PF}{PE}=\frac{PQ}{PC}$，即可得到结论；
（3）如图2，过P作PQ⊥BC交AB于Q，根据已知条件得到$\frac{PC}{PQ}$=n，根据余角的性质得到∠QPE=∠CPF，推出△PCF∽△PEQ，根据相似三角形的性质即可得到结论．

解答 解：（1）图中与△AFC相似的三角形为△PBE，
∵∠ACB=90°，
∴∠ACD+∠BCD=90°，
∵CD⊥AB于D，
∴∠B+∠BCD=90°，
∴∠ACD=∠B，
同理∠CAF=∠BPE，
∴△ACF∽△PBE；
故答案为：△PBE；

（2）如图1，过P作PQ⊥BC交AB于Q，
∵BC：AC=2，
∴BC=2AC，
∵P为BC的中点，
∴CP=BP=$\frac{1}{2}$BC，
∴AC=PC，
∴△ACP是等腰直角三角形，
∴∠CAF=∠APC=45°，
∵△ACF∽△PBE，
∴∠CAF=∠BPE=45°，∠AFC=∠BEP，
∴∠EPQ=∠CPF=45°，∠CFP=∠PEQ，
∴△PCF∽△PEQ，
∴$\frac{PF}{PE}=\frac{PQ}{PC}$，
∵PQ∥AC，
∴PQ=$\frac{1}{2}$AC=$\frac{1}{2}$PC，
∴PF：PE=2；

（3）如图2，过P作PQ⊥BC交AB于Q，
∴PQ∥AC，
∵BC：AC=n，
∴BC=nAC，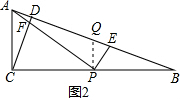
∵P为BC的中点，
∴PC=$\frac{1}{2}$BC=$\frac{n}{2}$AC，PQ=$\frac{1}{2}$AC，
∴$\frac{PC}{PQ}$=n，
∵∠BPE+∠QPE=∠BPE+∠CPF=90°，
∴∠QPE=∠CPF，
由（2）证得∠PFC=∠PEQ，
∴△PCF∽△PEQ，
∴$\frac{PF}{PE}=\frac{PC}{PQ}$=n．

点评 本题考查了相似三角形的判定和性质，垂直的定义，等腰直角三角形的性质，正确的作出辅助线是解题的关键．