
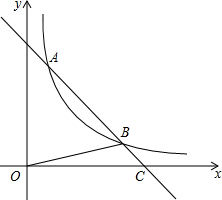
 如图,直线y=-x+5与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.若将直线y=-x+5向下平移1个单位,则所得直线与双曲线y=$\frac{k}{x}$(x>0)的交点有( )
如图,直线y=-x+5与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.若将直线y=-x+5向下平移1个单位,则所得直线与双曲线y=$\frac{k}{x}$(x>0)的交点有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 0个,或1个,或2个 |
分析 令直线y=-x+5与y轴的交点为点D,过点B作BE⊥x轴于点E,根据一次函数图象上点的坐标特征以及△BOC的面积是$\frac{5}{2}$即可得出BE的长度,进而可找出点B的坐标,根据反比例函数图象上点的坐标特征即可得出反比例函数系数k的值,根据平移的性质找出平移后的直线的解析式将其代入反比例函数解析式中,整理后根据根的判别式的正负即可得出结论.
解答 解:令直线y=-x+5与y轴的交点为点D,过点B作BE⊥x轴于点E,如图所示.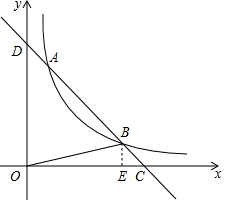
令直线y=-x+5中y=0,则0=-x+5,解得:x=5,
即OC=5.
∵△BOC的面积是$\frac{5}{2}$,
∴$\frac{1}{2}$OC•BE=$\frac{1}{2}$×5•BE=$\frac{5}{2}$,
解得:BE=1.
结合题意可知点B的纵坐标为1,
当y=1时,有1=-x+5,
解得:x=4,
∴点B的坐标为(4,1),
∴k=4×1=4,
即双曲线解析式为y=$\frac{4}{x}$.
将直线y=-x+5向下平移1个单位得到的直线的解析式为y=-x+5-1=-x+4,
将y=-x+4代入到y=$\frac{4}{x}$中,得:-x+4=$\frac{4}{x}$,
整理得:x2-4x+4=0,
∵△=(-4)2-4×4=0,
∴平移后的直线与双曲线y=$\frac{4}{x}$只有一个交点.
故选B.
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征以及三角形的面积公式,根据三角形的面积公式找出点B的坐标是解题的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
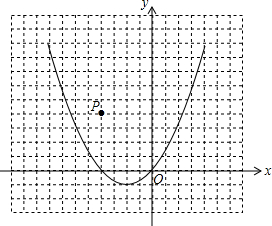 已知二次函数y=x2+x的图象,如图所示
已知二次函数y=x2+x的图象,如图所示查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 42 | B. | 49 | C. | 76 | D. | 77 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$或1 | B. | $\frac{1}{4}$或1 | C. | $\frac{3}{4}$或$\frac{1}{2}$ | D. | $\frac{1}{4}$或$\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…、则正方形OB2015B2016C2016的顶点B2016的坐标是(21008,0).
如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…、则正方形OB2015B2016C2016的顶点B2016的坐标是(21008,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
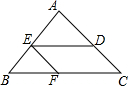 如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm.将线段DC沿着CB的方向平移7cm得到线段EF,点E,F分别落在边AB,BC上,则△EBF的周长为13cm.
如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm.将线段DC沿着CB的方向平移7cm得到线段EF,点E,F分别落在边AB,BC上,则△EBF的周长为13cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com