练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．下列运算正确的是（　　）
    A．8a2-4a=4aB．（-a3b）2=a6b2C．a-2+a2=a0D．a2•4a4=4a8

    分析 根据合并同类项、积的乘方、单项式乘单项式的运算法则分别计算，再作判断．

    解答 解：A、8a2，4a不是同类项，不能合并，故选项错误；
    B、（-a3b）2=a6b2，故选项正确；
    C、a-2，a2不是同类项，不能合并，故选项错误；
    D、a2•4a4=4a6，故选项错误．
    故选：B．

    点评 本题考查了合并同类项的法则，积的乘方、单项式乘单项式，熟练掌握运算性质是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    3．肥皂泡的泡壁厚度大约是0.0000007m，用科学记数法可表示为（　　）m．
    A．0.7×10-6B．0.7×10-7C．7×10-6D．7×10-7

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

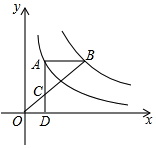    4．如图，点A在双曲线y=$\frac{4}{x}$上，点B在双曲线y=$\frac{k}{x}$（k≠0）上，AB∥x轴，过点A作AD⊥x轴于D．连接OB，与AD相交于点C，若AC=2CD，则k的值为（　　）
    A．6B．9C．10D．12

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

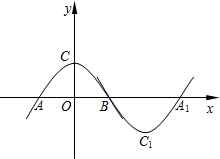    1．如图所示，抛物线l1：y=ax2+b（a＜0，b＞0）与x轴交于点A、B（点A在点B的左侧），与y轴交于点C，将抛物线l1绕点B旋转180°，得到新的抛物线l2，它的顶点为C1，与x轴的另一个交点为A1
    （1）当a=-1，b=1时，求B点坐标及抛物线l2的解析式；
    （2）若a=-$\frac{1}{2}$，且四边形AC1A1C为矩形，求抛物线l1的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

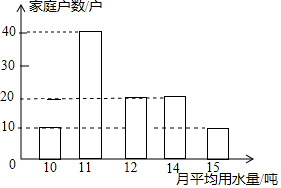    8．为了倡导“节约用水，从我做起”，市政府决定对市直机关500户家庭的用水情况作一次调查，市政府调查小组随机抽查了其中100户家庭一年的月平均用水量（单位：吨）．并将调查结果绘制成了如图所示的条形统计图，则这组数据的众数和中位数分别是（　　）
    A．40，20B．11，11C．11，12D．11，11.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

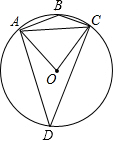    18．如图，⊙O是四边形ABCD的外接圆，连接AC，OA，OC，若∠ABC：∠ACO=13：4，则∠ADC的度数为（　　）
    A．30°B．50°C．40°D．45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，已知△ABC内接于⊙O，点C在劣弧AB上（不与点A，B重合），点D为弦BC的中点，DE⊥BC，DE与AC的延长线交于点E，射线AO与射线EB交于点F，与⊙O交于点G，设∠GAB=ɑ，∠ACB=β，∠EAG+∠EBA=γ，
    （1）点点同学通过画图和测量得到以下近似数据：
    ɑ30°40°50°60°
    β120°130°140°150°
    γ150°140°130°120°
    猜想：β关于ɑ的函数表达式，γ关于ɑ的函数表达式，并给出证明：
    （2）若γ=135°，CD=3，△ABE的面积为△ABC的面积的4倍，求⊙O半径的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图1所示，在△ABC中，点O是AC上一点，过点O的直线与AB，BC的延长线分别相交于点M，N．
    【问题引入】
    （1）若点O是AC的中点，$\frac{AM}{BM}$=$\frac{1}{3}$，求$\frac{CN}{BN}$的值；
    温馨提示：过点A作MN的平行线交BN的延长线于点G．
    【探索研究】
    （2）若点O是AC上任意一点（不与A，C重合），求证：$\frac{AM}{MB}$•$\frac{BN}{NC}$•$\frac{CO}{OA}$=1；
    【拓展应用】
    （3）如图2所示，点P是△ABC内任意一点，射线AP，BP，CP分别交BC，AC，AB于点D，E，F，若$\frac{AF}{BF}$=$\frac{1}{3}$，$\frac{BD}{CD}$=$\frac{1}{2}$，求$\frac{AE}{CE}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．有一组数据：2，5，5，6，7，这组数据的平均数为（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    同步练习册答案