
【题目】如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支经过AO的中点C,且与AB交于点D.
的图象的一支经过AO的中点C,且与AB交于点D.
(1)求反比例函数解析式
(2)若函数y=3x与y=![]() 的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比
的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比
【答案】
(1)
解:∵A点的坐标为(8,y),
∴OB=8,
∵AB⊥x轴于点B,sin∠OAB=![]() ,
,
∴![]() =
=![]() ,
,
∴OA=10,
由勾股定理得:AB=![]() =6,
=6,
∵点C是OA的中点,且在第一象限内,
∴C(4,3),
∵点C在反比例函数y=![]() 的图象上,
的图象上,
∴k=12,
∴反比例函数解析式为:y=![]() ;
;
(2)
解:将y=3x与y=![]() 联立成方程组,得:
联立成方程组,得:
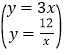 ,
,
解得:![]() ,
,![]() ,
,
∵M是直线与双曲线另一支的交点,
∴M(﹣2,﹣6),
∵点D在AB上,
∴点D的横坐标为8,
∵点D在反比例函数y=![]() 的图象上,
的图象上,
∴点D的纵坐标为![]() ,
,
∴D(8,![]() ),
),
∴BD=![]() ,
,
连接BC,如图所示,
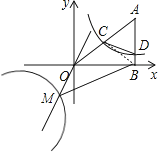
∵S△MOB=![]() 8|﹣6|=24,
8|﹣6|=24,
S四边形OCDB=S△OBC+S△BCD=![]() 83+
83+![]()
![]() 4=15,
4=15,
∴![]() .
.
【解析】(1)先根据锐角三角函数的定义,求出OA的值,然后根据勾股定理求出AB的值,然后由C点是OA的中点,求出C点的坐标,然后将C的坐标代入反比例函数y=![]() 中,即可确定反比例函数解析式;
中,即可确定反比例函数解析式;
(2)先将y=3x与y=![]() 联立成方程组,求出点M的坐标,然后求出点D的坐标,然后连接BC,分别求出△OMB的面积,△OBC的面积,△BCD的面积,进而确定四边形OCDB的面积,进而可求三角形OMB与四边形OCDB的面积的比.
联立成方程组,求出点M的坐标,然后求出点D的坐标,然后连接BC,分别求出△OMB的面积,△OBC的面积,△BCD的面积,进而确定四边形OCDB的面积,进而可求三角形OMB与四边形OCDB的面积的比.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
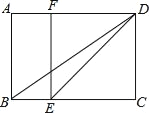
【题目】已知:如图,在矩形ABCD中,E是BC边一点,DE平分∠ADC,EF∥DC角AD边于点F,连结BD.
(1)求证:四边形EFCD是正方形;
(2)若BE=1,ED=2![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平行四边形ABCD中,对角线AC、BD交于点O,经过点O的直线AD于点E,交BC于点F.
(1)求证:OE=OF;
(2)如图2,连接AF、CE,当AF⊥FC时,在不添加辅助线的情况下,直接写出等于![]() 的线段.
的线段.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行比赛的路程与时间的关系如图所示.
(1)这是一场________米比赛;
(2)前一半赛程内________的速度较快,最终________赢得了比赛;
(3)两人第________秒在途中相遇,相遇时距终点________米;
(4)甲在前8秒的平均速度是多少?甲在整个赛程的平均速度是多少?乙在前8秒的平均速度是多少?乙在整个赛程的平均速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O,A,B,C的坐标分别为(0,0),(-1,2),(-3,3)和(-2,1).
(1)若图中的各个点的纵坐标不变,横坐标都乘-1,与原图案相比,所得图案有什么变化?画出图形并说明一下变化.
(2)若图中的各个点的横坐标不变,纵坐标都乘-1,与原图案相比,所得图案有什么变化?画出图形并说明一下变化.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两人是NBA联盟凯尔特人队的两位明星球员,两人在前五个赛季的罚球
命中率如下表所示:
甲球员的命中率(%) | 87 | 86 | 83 | 85 | 79 |
乙球员的命中率(%) | 87 | 85 | 84 | 80 | 84 |
(1)分别求出甲,乙两位球员在前五个赛季罚球的平均命中率;
(2)在某场比赛中,因对方球员技术犯规需要凯尔特人队选派一名队员进行罚球,你认为甲,乙两位球员谁来罚球更好?(请通过计算说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABC绕点C顺时针旋转120得到 ![]() EDC,连接AD,BD.
EDC,连接AD,BD.
则下列结论:
①AC=AD;
②BD ![]() AC;
AC;
③四边形ACED是菱形.
其中正确的个数是( )
A.O
B.1
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
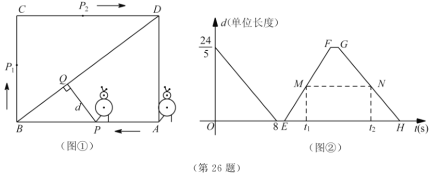
【题目】某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点![]() 出发,在矩形
出发,在矩形![]() 边上沿着
边上沿着![]() 的方向匀速移动,到达点
的方向匀速移动,到达点![]() 时停止移动.已知机器人的速度为
时停止移动.已知机器人的速度为![]() 个单位长度/
个单位长度/![]() ,移动至拐角处调整方向需要
,移动至拐角处调整方向需要![]()
![]() (即在
(即在![]() 、
、![]() 处拐弯时分别用时
处拐弯时分别用时![]()
![]() ).设机器人所用时间为
).设机器人所用时间为![]() 时,其所在位置用点
时,其所在位置用点![]() 表示,
表示,![]() 到对角线
到对角线![]() 的距离(即垂线段
的距离(即垂线段![]() 的长)为
的长)为![]() 个单位长度,其中
个单位长度,其中![]() 与
与![]() 的函数图像如图②所示.
的函数图像如图②所示.
(1)求![]() 、
、![]() 的长;
的长;
(2)如图②,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,线段
上,线段![]() 平行于横轴,
平行于横轴,![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() 、
、![]() .设机器人用了
.设机器人用了![]() 到达点
到达点![]() 处,用了
处,用了![]() 到达点
到达点![]() 处(见图①).若
处(见图①).若![]() ,求
,求![]() 、
、![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com