
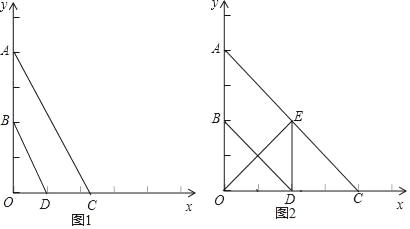
【题目】已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.
(1)求证:BD∥AC;
(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;
(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
【答案】(1)BD∥AC;(2)点C的坐标为(![]() ,0);(3)直线AC的解析式为y=﹣x+4.
,0);(3)直线AC的解析式为y=﹣x+4.
【解析】试题分析:(1)由A与B的坐标求出OA与OB的长,进而得到B为OA的中点,而D为OC的中点,利用中位线定理即可得证;
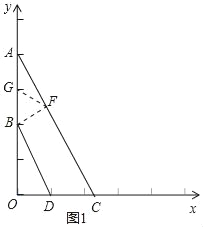
(2)如图1,作BF⊥AC于点F,取AB的中点G,确定出G坐标,由平行线间的距离相等求出BF的长,在直角三角形ABF中,利用斜边上的中线等于斜边的一半求出FG的长,进而确定出三角形BFG为等边三角形,即∠BAC=30°,设OC=x,则有AC=2x,利用勾股定理表示出OA,根据OA的长求出x的值,即可确定出C坐标;
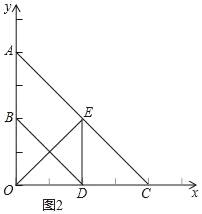
(3)如图2,当四边形ABDE为平行四边形时,AB∥DE,进而得到DE垂直于OC,再由D为OC中点,得到OE=CE,再由OE垂直于AC,得到三角形AOC为等腰直角三角形,求出OC的长,确定出C坐标,设直线AC解析式为y=kx+b,将A与C坐标代入求出k与b的值,即可确定出AC解析式.
试题解析:
(1)∵A(0,4),B(0,2),
∴OA=4,OB=2,点B为线段OA的中点,
又点D为OC的中点,即BD为△AOC的中位线,
∴BD∥AC;
(2)如图1,作BF⊥AC于点F,取AB的中点G,则G(0,3),
∵BD∥AC,BD与AC的距离等于1,
∴BF=1,
∵在Rt△ABF中,∠AFB=90°,AB=2,点G为AB的中点,
∴FG=BG=![]() AB=1,
AB=1,
∴△BFG是等边三角形,∠ABF=60°.
∴∠BAC=30°,
设OC=x,则AC=2x,
根据勾股定理得:OA=![]() ,
,
∵OA=4,
∴x=![]() ,
,
∵点C在x轴的正半轴上,
∴点C的坐标为(![]() ,0);
,0);
(3)如图2,当四边形ABDE为平行四边形时,AB∥DE,
∴DE⊥OC,
∵点D为OC的中点,
∴OE=EC,
∵OE⊥AC,
∴∠OCA=45°,
∴OC=OA=4,
∵点C在x轴的正半轴上,
∴点C的坐标为(4,0),
设直线AC的解析式为y=kx+b(k≠0).
将A(0,4),C(4,0)代入AC的解析式得:
![]()
解得:![]()
∴直线AC的解析式为y=﹣x+4.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
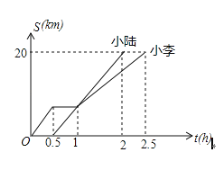
【题目】小李与小陆从A地出发,骑自行车沿同一条路行驶到B地,他们离出发地的距离S(单位:km)和行驶时间t(单位:h)之间的函数关系的图象如图所示,根据图中提供的信息,有下列说法:
(1)他们都行驶了20km;
(2)小陆全程共用了1.5h;
(3)小李与小陆相遇后,小李的速度小于小陆的速度;
(4)小李在途中停留了0.5h.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
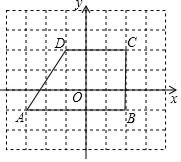
【题目】在直角坐标平面里,梯形ABCD各顶点的位置如图所示,图中每个小正方形方格的边长为1个单位长度.
(1)求梯形ABCD的面积;
(2)如果把梯形ABCD在坐标平面里先向右平移1个单位,然后向下平移2个单位得到梯形A1B1C1D1,求新顶点A1,B1,C1,D1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.

(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业去年的年产值为a亿元,今年增长率为x,如果明年还能按这个速度增长,那么预计明年的年产值为( )亿元.
A.a(1+2x)
B.2a(1+x%)
C.a(1+x)2
D.a+2x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,二次函数y=ax2﹣5x+c的图象如图.
(1)求这个二次函数的解析式
(2)观察图象,回答:何时y随x的增大而增大;何时y随x的增大而减小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°.点D到地面的垂直距离![]() ,求点B到地面的垂直距离BC.
,求点B到地面的垂直距离BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个四边形的一条对角线把四边形分成两个等腰三角形,且其中一个等腰三角形的底角是另一个等腰三角形底角的2倍,我们把这条对角线叫做这个四边形的黄金线,这个四边形叫做黄金四边形.

(1)如图1,在四边形ABCD中,AB=AD=DC,对角线AC,BD都是黄金线,且AB<AC,CD<BD,求四边形ABCD各个内角的度数;
(2)如图2,点B是弧AC的中点,请在⊙O上找出所有的点D,使四边形ABCD的对角线AC是黄金线(要求:保留作图痕迹);
(3)在黄金四边形ABCD中,AB=BC=CD,∠BAC=30°,求∠BAD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com