
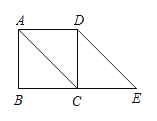
【题目】过正方形ABCD的顶点D作DE∥AC,交BC的延长线于点E.
(1)判断四边形ACED的形状,并说明理由;
(2)若CE=4,求AC的长.
科目:初中数学 来源: 题型:
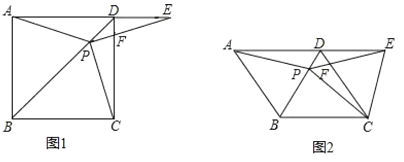
【题目】如图①,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且PC=PE,PE交CD于点F.
(1)求证:∠PCD=∠PED;
(2)连接EC,求证:EC=![]() AP;
AP;
(3)如图②,把正方形ABCD改成菱形ABCD,其他条件不变,当∠DAB=60°时,请直接写出线段EC和AP的数量关系______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快“秀美荆河水系生态治理工程”进度,污水处理厂决定购买10台污水处理设备.现有A,B两种型号的设备,每台的价格分别为a万元,b万元,每月处理污水量分别为240吨,200吨.已知购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求a,b的值;
(2)厂里预算购买污水处理设备的资金不超过105万元,你认为有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为污水处理厂设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
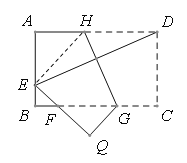
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上E处,EQ与BC相交于F,若AD=8 cm,AB=6 cm,AE=4cm,则△EBF的周长是______________ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
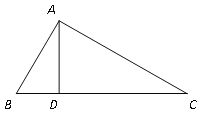
【题目】如图,△ABC中,![]() ,AD是BC边上的高,如果
,AD是BC边上的高,如果![]() ,我们就称△ABC为“高和三角形”.请你依据这一定义回答问题:
,我们就称△ABC为“高和三角形”.请你依据这一定义回答问题:
(1)若![]() ,
,![]() ,则△ABC____ “高和三角形”(填“是”或“不是”);
,则△ABC____ “高和三角形”(填“是”或“不是”);
(2)一般地,如果△ABC是“高和三角形”,则![]() 与
与![]() 之间的关系是____,并证明你的结论
之间的关系是____,并证明你的结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )
A. b≥![]() B. b≥1或b≤﹣1 C. b≥2 D. 1≤b≤2
B. b≥1或b≤﹣1 C. b≥2 D. 1≤b≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△MNP中,∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至点G,取NG=NQ,若△MNP的周长为12,MQ=a,则△MGQ周长是 ( )

A.8+2aB.8aC.6+aD.6+2a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com