
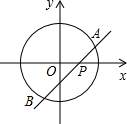
 如图,在平面直角坐标系中,已知⊙O的半径为2,动直线AB与x轴交于点P(x,0),直线AB与x轴正方向夹角为45°,若直线AB与⊙O有公共点,则x的取值范围是( )
如图,在平面直角坐标系中,已知⊙O的半径为2,动直线AB与x轴交于点P(x,0),直线AB与x轴正方向夹角为45°,若直线AB与⊙O有公共点,则x的取值范围是( )| A. | -2≤x≤2 | B. | -2$\sqrt{2}$<x<2$\sqrt{2}$ | C. | 0≤x≤2$\sqrt{2}$ | D. | -2$\sqrt{2}$≤x≤2$\sqrt{2}$ |
分析 将动直线AB向上或向下平移,因为直线AB与⊙O有公共点,可以有一个或两个,即直线与⊙O相交或相切;分别计算相切时所对应的x的值,写出x的取值范围即可.
解答 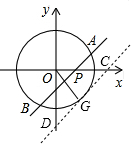 解:如图所示,当AB与⊙O相切时,有一个公共点,设这个公共点为G,连接OG,则OG⊥CD,
解:如图所示,当AB与⊙O相切时,有一个公共点,设这个公共点为G,连接OG,则OG⊥CD,
这时OG=2,∠OCD=45°,
sin45°=$\frac{OG}{OC}$,
OC=$\frac{2}{\frac{\sqrt{2}}{2}}$=2$\sqrt{2}$,
即x=2$\sqrt{2}$,
如果直线AB在第二象限与圆相切,这时同理可求得x=-2$\sqrt{2}$,
∴x的取值范围是-2$\sqrt{2}$≤x≤2$\sqrt{2}$,
故选D.
点评 本题考查了直线与圆的位置关系,明确直线和圆的三种位置关系:①相离:一条直线和圆没有公共点.②相切:一条直线和圆只有一个公共点,叫做这条直线和圆相切,③相交:一条直线和圆有两个公共点,此时叫做这条直线和圆相交;当直线AB与x轴正方向夹角为45°时,可以理解为所构成的三角形的关系,也可以理解为直线AB与直线y=x平行.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 5.97×107 | B. | 6.0×107 | C. | 5.97×108 | D. | 6.0×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com