Question

2．如图①，矩形ABCD中，AB=12，AD=25，延长CB至E，使BE=9，连接AE，将△ABE沿AB翻折使点E落在BC上的点F处，连接DF．△ABE从点B出发，沿线段BC以每秒3个单位的速度平移得到△A′B′E′，当点E′到达点F时，△ABE又从点F开始沿射线FD方向以每秒5个单位的速度平移，当点E′到达点D时停止运动，设运动的时间为t秒．
（1）线段DF的长度为20；当f=$\frac{31}{4}$秒时，点B′落在CD上；
（2）在△ABE平移的过程中，记△A′B′E′与△AFD互相重叠部分的面积为S，请直接写出面积S与运动时
间t之间的函数关系式，并写出自变量t的取值范围；
（3）如图②，当点E′到达点F时，△ABE从点F开始沿射线FD方向以每秒5个单位的速度平移时，设A′B′
交射线FD于点M，交线段AD于点N，是否存在某一时刻t，使得△DMN为等腰三角形？若存在，请求出相应的t值；若不存在，请说明理由．
 

Answer 1

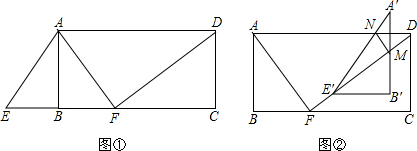
分析 （1）由对折得到BF=BE=9，再由△E′DB′∽△FDC得到比例式，求出FE′即可；
（2）分四种情况①当0＜t≤3时，②当3＜t≤6时，③当6＜t≤$\frac{31}{4}$时，④当$\frac{31}{4}$＜t≤10时，都根据相似列出比例式，求出相关线段即可；
（3）分三种情况计算：①当DM=DN时，②当DM=MN时，③当DN=DM时，利用三角形相似和矩形的性质计算即可．

解答 解：如图1，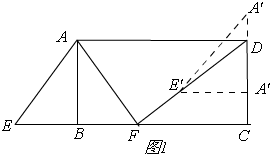

（1）由对折得，BF=BE=9，
∴CF=BC-BF=16，DC=AB=12，
∴DF=20，
∵沿线段BC以每秒3个单位的速度平移得到△A′B′E′，
∴E′到达点F的距离为9×2=18，
∴t_BF=$\frac{18}{3}$=6，
当点B′落在CD上时，△E′DB′∽△FDC，
∴$\frac{E′D}{FD}=\frac{E′B′}{FC}$，
∴$\frac{E′D}{20}=\frac{9}{16}$，
∴E′D=$\frac{45}{4}$，
∴FE′=FD-E′D=$\frac{35}{4}$，
∴在FE′段一段时间为t_FE′=$\frac{35}{4}÷5$=$\frac{7}{4}$，
∴t=t_BF+t_FE′=$\frac{31}{4}$，
（2）分四种情况，
①如图2，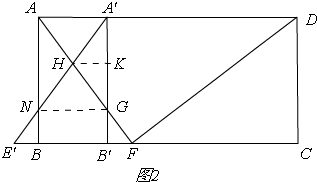

当0＜t≤3时，作NG⊥A′B′，
∴△A′GN∽△A′B′E′，
∴$\frac{A′G}{A′B′}=\frac{NG}{E′B′}$，
∴$\frac{A′G}{12}=\frac{3t}{9}$，
∴A′G=4t，
作GK⊥A′B′，
∴HK=$\frac{1}{2}$BB′=$\frac{3t}{2}$，
∴S=$\frac{1}{2}$A′G×KH=3t²，
②如图3，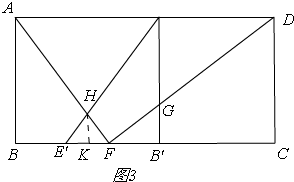

当3＜t≤6时，B′B=3t，FB=9，FB′=BB′-FB=3t-9，
∵△FB′G∽△FCD，
∴$\frac{FB′}{FC}=\frac{GB′}{CD}$，
∴$\frac{3t-9}{16}=\frac{GB′}{12}$，
∴GB′=$\frac{3}{4}$（3t-9），
∴S_△FB′G=$\frac{1}{2}$FB′×GB′=$\frac{3}{8}$（3t-9）²，
作KH⊥E′F，
∴K为BB′的中点，
∴KB′=$\frac{1}{2}$BB′=$\frac{3}{2}$t，
∴E′K=E′B′-KB′=9-$\frac{3}{2}$t，
∵△E′KH∽△E′B′A′，
∴$\frac{KH}{B′A′}=\frac{E′K}{E′B′}$，
∴$\frac{KH}{12}=\frac{9-\frac{3}{2}t}{9}$，
∴KH=$\frac{4}{3}$（9-$\frac{3}{2}$t），
∵FB′=3t-9，
∴E′F=E′B′-FB′=9-（3t-9）=18-3t，
∴S_△E′FH=$\frac{1}{2}$E′F×KH=$\frac{1}{3}$（18-3t）²，
∴S=S_{△A′B′E′}-S_△FB′G=-$\frac{51}{8}$t2+$\frac{225}{4}$t-$\frac{675}{8}$（3＜t≤6）
③如图4，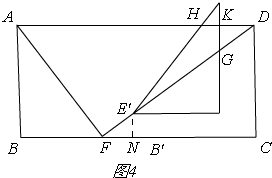

当6＜t≤$\frac{31}{4}$时，
同②的方法，S=-$\frac{27}{8}$t²+$\frac{81}{2}$t-$\frac{783}{8}$（6＜t≤$\frac{31}{4}$），
④如图5，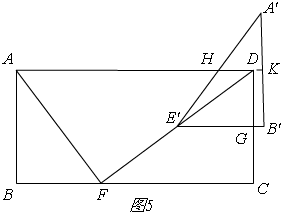

当$\frac{31}{4}$＜t≤10时，
同②的方法，S=$\frac{21}{8}$t²-$\frac{105}{2}$t+$\frac{525}{2}$，
（3）由（1）（2）知，CF=16，DC=12，DF=20，FE′=5（t-6），
分三种情况，
①当DM=DN时，如图6，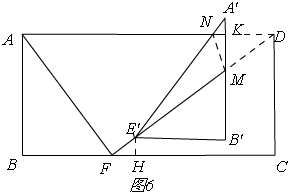

作E′F⊥FC，
∴△FE′H∽△FDC，
∴$\frac{FE′}{FD}=\frac{FH}{FC}=\frac{E′H}{DC}$．
∴$\frac{5（t-6）}{20}=\frac{FH}{16}=\frac{E′H}{12}$，
∴FH=4（t-6），E′H=3（t-6），
∴DK=CF-B′E′-FH=31-4t，
∵A′B=CD，
∴A′K+KB′=KB′=E′H，
∴A′K=E′H=3（t-6），
∵△A′KN∽△A′B′E′，
∴$\frac{NK}{E′B′}=\frac{A′K}{A′B′}$
∴$\frac{NK}{9}=\frac{3（t-6）}{12}$，
∴NK=$\frac{9（t-6）}{4}$，
∴DN=DK+KN=-$\frac{7}{4}$t+$\frac{35}{2}$，
∵△E′B′M∽△FCD，
∴$\frac{E′M}{FD}=\frac{E′B′}{FC}$，
∴E′M=$\frac{45}{4}$，
∴DM=FD-FE′=$\frac{155}{4}$-5t，
∵DM=DN，
∴$\frac{155}{4}$-5t=-$\frac{7}{4}$t+$\frac{35}{2}$，
∴t=$\frac{85}{13}$．
②当DM=MN时，如图7，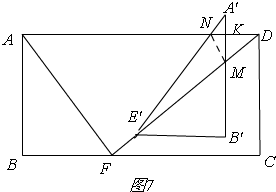

∵DM=NM，
∴DK=NK，
由①有，DK=31-4t，NK=$\frac{9（t-6）}{4}$，
∴31-4t=$\frac{9（t-6）}{4}$，
∴t=$\frac{178}{25}$，
③当DN=DM 时，如图8，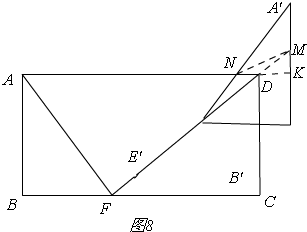

DE′=DF-FE′=50-5t，
∵△DE′G∽△DFC，
∴$\frac{DG}{DC}=\frac{E′}{FC}=\frac{DE′}{DF}$，
∴$\frac{DG}{12}=\frac{E′G}{16}=\frac{50-5t}{20}$，
∴DG=30-3t，E′G=40-4t，
∵DKB′G是矩形，
∴KB′=30-3t，
DK=GB′=E′B′-E′G=4t-31，
∵△ME′B′∽△DFC，
∴$\frac{E′M}{FD}=\frac{E′B′}{FC}$，
∴$\frac{E′M}{20}=\frac{9}{16}$，
∴E′M=$\frac{45}{4}$，
∵△MDK∽△ME′B′，
∴$\frac{MD}{NE′}=\frac{DK}{E′B′}$，
∴MD=5t-$\frac{155}{4}$，
∵△A′KN∽△A′B′E′，
∴$\frac{KN}{9}=\frac{3t-18}{12}$，
∴KN=$\frac{9t-54}{4}$，
∴DN=KN-KD=-$\frac{7}{4}$t+$\frac{35}{2}$，
∵DN=DM，
∴5t-$\frac{155}{4}$=-$\frac{7}{4}$t+$\frac{35}{2}$，
∴t=$\frac{25}{3}$

点评 此题是四边形综合题，主要考查了矩形的性质，相似三角形的性质和判定，解本题的关键是作出辅助线．