
【题目】如图,为了测得某建筑物的高度![]() ,在
,在![]() 处用高为
处用高为![]() 米的测角仪
米的测角仪![]() ,测得该建筑物顶端
,测得该建筑物顶端![]() 的仰角为
的仰角为![]() ,再向建筑物方向前进
,再向建筑物方向前进![]() 米,又测得该建筑物顶端
米,又测得该建筑物顶端![]() 的仰角为
的仰角为![]() .
.
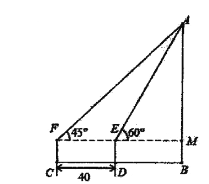
(1)填空:![]() ,
,![]() ;
;
(2)求该建筑物的高度![]() .(结果保留根号)
.(结果保留根号)
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的四个顶点都在双曲线y=![]() (k>0)上,BC=2AB,且矩形ABCD的面积是32,则k的值是( )
(k>0)上,BC=2AB,且矩形ABCD的面积是32,则k的值是( )
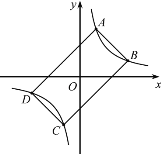
A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
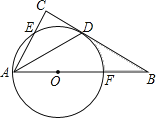
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018无锡市体育中考男生项目分为速度耐力类、力量类和灵巧类,每位考生只能在三类中各选一项进行考试.其中速度耐力类项目有:50米跑、800米跑、50米游泳;力量类项目有:掷实心球、引体向上;灵巧类项目有:30秒钟跳绳、立定跳远、俯卧撑、篮球运球.男生小明“50米跑”是强项,他决定必选,其它项目在平时测试中成绩完全相同,他决定随机选择.
(1)请用画树状图或列表的方法求“小明‘选50米跑、引体向上和立定跳远’”的概率;
(2)小明所选的项目中有立定跳远的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别相交于点
轴分别相交于点![]() .点
.点![]() 是
是![]() 轴上动点,点
轴上动点,点![]() 从点
从点![]() 出发向原点O运动,点
出发向原点O运动,点![]() 在点
在点![]() 右侧,
右侧,![]() .过点
.过点![]() 作
作![]() 于点
于点![]() 将
将![]() 沿直线
沿直线![]() 翻折,得到
翻折,得到![]() 连接
连接![]() .设
.设![]()
![]() 与
与![]() 重合部分面积为
重合部分面积为![]() 求:
求:
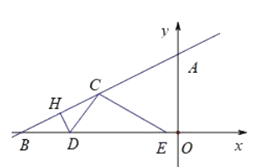
(1)求线段![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 关于
关于![]() 的函数解析式,并直接写出自变量
的函数解析式,并直接写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
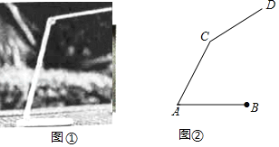
【题目】图①是放置在水平面上的台灯,图②是其侧面示意图(台灯底座高度忽略不计),其中灯臂AC=44cm,灯罩CD=32cm,灯臂与底座构成的∠CAB=60°.CD可以绕点C上下调节一定的角度.使用发现:当CD与水平线所成的角为30°时,台灯光线最佳.现测得点D到桌面的距离为54.06cm.请通过计算说明此时台灯光线是否为最佳?(参考数据:![]() 取1.73).
取1.73).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com