
分析 (1)先去分母,然后移项,合并同类项,系数化为1求解即可.
(2)先求出两个不等式的解集,再求其公共解.
解答 解:(1)去分母得:4x-2-15x-3≤6,
移项合并同类项得:-11x≤11,
系数化为1得:x≥1.
(2)$\left\{\begin{array}{l}{5x+2>4x①}\\{3(5-3x)≥10-4x②}\end{array}\right.$,
由①得 x>-2,
由②得,x≤1,
所以,原不等式组的解集为-2<x≤1.
点评 本题主要考查了一元一次不等式(组)解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).


科目:初中数学 来源: 题型:解答题
| x | 50 | 80 | 100 | 120 |
| y | 40 | 34 | 30 | 26 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
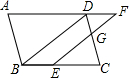 如图,平行四边形ABCD,点E在边BC上,点F在AD边的延长线上,且EF∥BD,EF,CD交于点G,$\frac{DF}{AD}$=$\frac{2}{5}$,S四边形BDGE=a,则S平行四边形ABCD的值为( )
如图,平行四边形ABCD,点E在边BC上,点F在AD边的延长线上,且EF∥BD,EF,CD交于点G,$\frac{DF}{AD}$=$\frac{2}{5}$,S四边形BDGE=a,则S平行四边形ABCD的值为( )| A. | $\frac{25a}{8}$ | B. | $\frac{25a}{9}$ | C. | $\frac{25a}{16}$ | D. | $\frac{16a}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
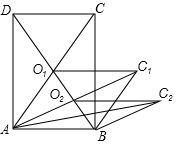 如图所示,矩形ABCD的面积为12cm2,它的两条对角线交于点O1,以AB、AO1邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2;同样以AB、AO2为邻边作平行四边形ABC2O2…;依此类推,则平行四边形ABC6O6的面积为$\frac{3}{16}$cm2.
如图所示,矩形ABCD的面积为12cm2,它的两条对角线交于点O1,以AB、AO1邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2;同样以AB、AO2为邻边作平行四边形ABC2O2…;依此类推,则平行四边形ABC6O6的面积为$\frac{3}{16}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
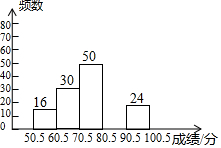 某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.
某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.| 组别 | 分数段 | 频数 | 频率 |
| 一 | 50.5-60.5 | 16 | 0.08 |
| 二 | 60.5-70.5 | 30 | 0.15 |
| 三 | 70.5-80.5 | 50 | 0.25 |
| 四 | 80.5-90.5 | m | 0.40 |
| 五 | 90.5-100.5 | 24 | n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
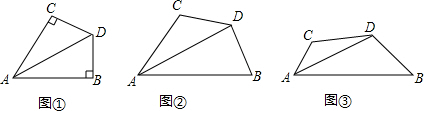
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com