
【题目】如图,在矩形ABCD中,AB:BC=3:5,点E是对角线BD上一动点(不与点B,D重合),将矩形沿过点E的直线MN折叠,使得点A,B的对应点G,F分别在直线AD与BC上,当△DEF为直角三角形时,CN:BN的值为______.
【答案】![]() 或
或![]()
【解析】
因为点A,B的对应点G,F分别在直线AD与BC上,所以分两种情况讨论, 当∠EFD=90°时,证明△EFN∽△FDC,设CD=5a,根据比例式表示出CN,BN即可;当∠EDF=90°时,证明△FCD∽△DCB,设CD=3a, 根据比例式表示出CN,BN即可.
解:分两种情况:
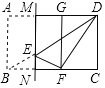
当∠EFD=90°时,如下图,

∵∠EFN=∠C=90°,易证∠EFN=∠FDC,
∴△EFN∽△FDC,
设CD=5a,由题可知,CF=3a,
∴![]() ,∴BC=
,∴BC=![]() ,
,
∴BN=NF=![]() ,即
,即![]()
当∠EDF=90°时,如下图,
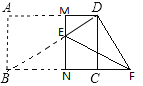
同理易证:△FCD∽△DCB,
设CD=3a,则BC=5a,CF=![]()
∴BF=5a+![]() ,
,
∴BN=![]() ,NC=
,NC=![]() ,
,
∴![]()
综上, CN:BN的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上(点A与点B不重合),我们定义:这样的两条抛物L1,L2互为“友好”抛物线,可见一条抛物线的“友好”抛物线可以有多条.
(1)如图2,已知抛物线L3:y=2x2-8x+4与y轴交于点C,试求出点C关于该抛物线对称轴对称的点D的坐标;
(2)请求出以点D为顶点的L3的友好抛物线L4的解析式,并指出L3与L4中y同时随x增大而增大的自变量的取值范围;
(3)若抛物y=a1 (x-m) 2+n的任意一条友好抛物线的解析式为y=a2 (x-h) 2+k,请写出a1与a2的关系式,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
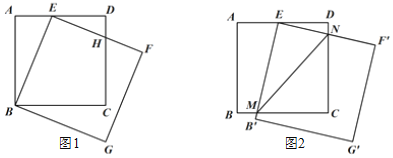
【题目】如图1,在正方形ABCD中,AB=3,E是AD边上的一点(E与A、D不重合),以BE为边画正方形BEFG,边EF与边CD交于点H.
(1)当E为边AD的中点时,求DH的长;
(2)设DE=x,CH=y,求y与x之间的函数关系式,并求出y的最小值;
(3)若DE=![]() ,将正方形BEFG绕点E逆时针旋转适当角度后得到正方形B'EF'G',如图2,边EF'与CD交于点N、EB'与BC交于点M,连结MN,求∠ENM的度数.
,将正方形BEFG绕点E逆时针旋转适当角度后得到正方形B'EF'G',如图2,边EF'与CD交于点N、EB'与BC交于点M,连结MN,求∠ENM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
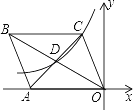
【题目】如图,OABC中顶点A在x轴负半轴上,B、C在第二象限,对角线交于点D,若C、D两点在反比例函数![]() 的图象上,且OABC的面积等于12,则k的值是____.
的图象上,且OABC的面积等于12,则k的值是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店经销甲、乙两种不同的笔记本.已知:两种笔记本的进价之和为10元,甲种笔记本每本获利2元,乙种笔记本每本获利1元,马阳光同学买4本甲种笔记本和3本乙种笔记本共用了47元.
(1)甲、乙两种笔记本的进价分别是多少元?
(2)该文具店购入这两种笔记本共60本,花费不超过296元,则购买甲种笔记本多少本时该文具店获利最大?
(3)店主经统计发现平均每天可售出甲种笔记本350本和乙种笔记本150本.如果甲种笔记本的售价每提高1元,则每天将少售出50本甲种笔记本;如果乙种笔记本的售价每提高1元,则每天少售出40本乙种笔记本,为使每天获取的利润更多,店主决定把两种笔记本的价格都提高![]() 元,在不考虑其他因素的条件下,当
元,在不考虑其他因素的条件下,当![]() 定为多少元时,才能使该文具店每天销售甲、乙两种笔记本获取的利润最大?
定为多少元时,才能使该文具店每天销售甲、乙两种笔记本获取的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推进球类运动的发展,某校组织校内球类运动会,分篮球、足球、排球、羽毛球、乒乓球五项,要求每位学生必须参加一项并且只能参加一项,某班有一名学生根据自己了解的班内情况绘制了如图所示的不完整统计表和扇形统计图.

请根据图表中提供的信息,解答下列问题:
(1)图表中m=________,n=________;
(2)若该校学生共有1000人,则该校参加羽毛球活动的人数约为________人;
(3)该班参加乒乓球活动的4位同学中,有3位男同学(分别用A,B,C表示)和1位女同学(用D表示),现准备从中选出两名同学参加双打比赛,用树状图或列表法求出恰好选出一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本![]() (单位:元)、销售价
(单位:元)、销售价![]() (单位:元)与产量x(单位:kg)之间的函数关系.
(单位:元)与产量x(单位:kg)之间的函数关系.
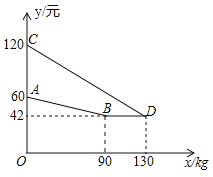
(1)请解释图中点D的横坐标、纵坐标的实际意义;
(2)求线段AB所表示的![]() 与x之间的函数表达式;
与x之间的函数表达式;
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
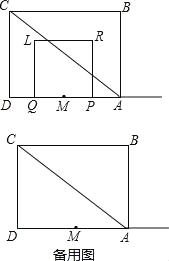
【题目】如图,四边形ABCD为矩形,AC为对角线,AB=6,BC=8,点M是AD的中点,P、Q两点同时从点M出发,点P沿射线MA向右运动;点Q沿线段MD先向左运动至点D后,再向右运动到点M停止,点P随之停止运动.P、Q两点运动的速度均为每秒1个单位.以PQ为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与△ABC重叠部分的面积为S.
(1)当点R在线段AC上时,求出t的值.
(2)求出S与t之间的函数关系式,并直接写出取值范围.(求函数关系式时,只须写出重叠部分为三角形时的详细过程,其余情况直接写出函数关系式.)
(3)在点P、点Q运动的同时,有一点E以每秒1个单位的速度从C向B运动,当t为何值时,△LRE是等腰三角形.请直接写出t的值或取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com