
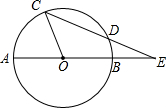
 如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=87°,则∠E等于( )
如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=87°,则∠E等于( )| A. | 42° | B. | 29° | C. | 21° | D. | 20° |
分析 利用半径相等得到DO=DE,则∠E=∠DOE,根据三角形外角性质得∠1=∠DOE+∠E,所以∠1=2∠E,同理得到∠AOC=∠C+∠E=3∠E,然后利用∠E=$\frac{1}{3}$∠AOC进行计算即可.
解答 解:连结OD,如图,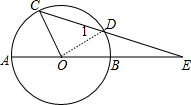
∵OB=DE,OB=OD,
∴DO=DE,
∴∠E=∠DOE,
∵∠1=∠DOE+∠E,
∴∠1=2∠E,
而OC=OD,
∴∠C=∠1,
∴∠C=2∠E,
∴∠AOC=∠C+∠E=3∠E,
∴∠E=$\frac{1}{3}$∠AOC=$\frac{1}{3}$×87°=29°.
故选B.
点评 本题考查了圆的认识:掌握与圆有关的概念( 弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.


科目:初中数学 来源: 题型:填空题
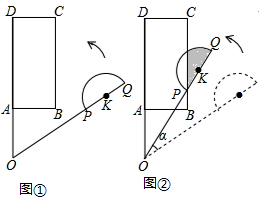 平面上,矩形ABCD与直径为QP的半圆K如图如图①摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针开始旋转,如图②,当点P恰好落在BC边上时,S阴影=$\frac{π}{24}$+$\frac{\sqrt{3}}{16}$.
平面上,矩形ABCD与直径为QP的半圆K如图如图①摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针开始旋转,如图②,当点P恰好落在BC边上时,S阴影=$\frac{π}{24}$+$\frac{\sqrt{3}}{16}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com