
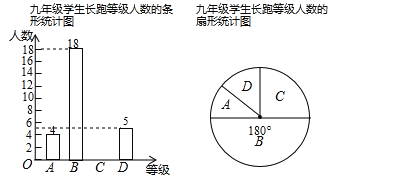
����Ŀ��ij��ѧΪ���˽���꼶ѧ�������ܡ��ɼ�������������ȡ���־��꼶ѧ���������䳤�ܳɼ�(����1000�ף�Ů��800��)�������ܳɼ����η�ΪA��B��C��D�ĸ��ȼ�����ͳ�ƣ���������������������ͳ��ͼ��
����������Ϣ������������⣺
(1)������ͳ��ͼ�У�![]() ��Ӧ������Բ�Ľ���______�ȣ�
��Ӧ������Բ�Ľ���______�ȣ�
(2)��ȫ����ͳ��ͼ��
(3)����ȡѧ���ġ����ܡ����Գɼ�����λ��������______�ȼ���
(4)��У���꼶��477��ѧ��,����ơ����ܡ����Գɼ��ﵽ![]() ����ѧ��Լ�ж����ˣ�
����ѧ��Լ�ж����ˣ�
���𰸡�(1)90 (2)������ (3)B (4)53��
��������
(1)����ͳ��ͼ�е����ݿ�����ñ��ε����������Ȼ�������C�ȼ����������Ӷ��������������ͳ��ͼ�У�C��Ӧ������Բ�ĽǵĶ�����
(2)����(1)���C�ȼ������������ɽ�����ͳ��ͼ����������
(3)����ͳ��ͼ�е����ݿ��Եõ�����ȡѧ���������������Գɼ�����λ���������ĸ��ȼ���
(4)����ͳ��ͼ�е����ݿ��Լ���������������Գɼ��ﵽA����ѧ���ж����ˣ�
��:((1)������������18��![]() ��36��
��36��
C�ȼ�������Ϊ��36��4��18��5��9��
��������ͳ�����У�C��Ӧ������Բ�Ľ��ǣ�![]() ��360��90����
��360��90����
�ʴ�Ϊ90��
(2)��ͼ(��ͼ�淶,��ʾ9��)
(3)��ͳ��ͼ�ɵã�
����ȡѧ���������������Գɼ�����λ��������B�ȼ���
�ʴ�ΪB��
(4)477��(4��36)=53
��:���Գɼ��ﵽA����ѧ����53��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������۸��ܷ�����������Ӱ�죬�нϴ���ȵ�������Ϊ�˽�ij������ֳ���ܷ������������Ⱦ����������ִӸõ�����������ֳ���������ȡ�˲�����ֳ�������˵��飨�ѵ�������Ϊ�ĸ��ȼ���A�����dz����أ�B�������أ�C����һ�㣻D����û�и�Ⱦ�����������������Ƴ�����������������ͳ��ͼ�������ͳ��ͼ�е���Ϣ����������⣺
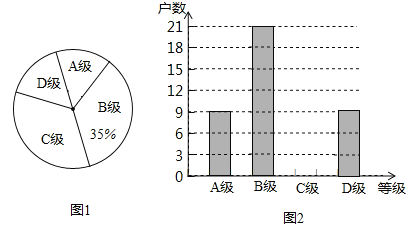
��1�����γ����������ֳ�����ܻ������� ������ͼ2����ͳ��ͼ����������
��2�����õ�����������ֳ����1500������dz����������ص���ֳ��һ���ж��ٻ���
��3��ij���е�λ���5��������ֳ�����ֱ��Ϊa��b��c��d��e�������ѡȡ��������һ�����ټ�ⲡ����������������б�����״ͼ�ķ������ѡ����ֳ��e�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�CA��CB����ACB��������P ��ƽ���ڲ����A��C �غϵ�����һ�㣬����AP�����߶�AP �Ƶ�P ��ʱ����ת���õ��߶�DP������AD��BD��CP��
��1������۲죺��ͼ1��������60��ʱ��![]() ��ֵ��________��ֱ��BD��ֱ��CP�ཻ���ɵĽ�С�ǵĶ�����________��
��ֵ��________��ֱ��BD��ֱ��CP�ཻ���ɵĽ�С�ǵĶ�����________��
��2�����̽������ͼ2��������90��ʱ����д��![]() ��ֵ��ֱ��BD��ֱ��CP�ཻ���ɵĽ�С�ǵĶ���������ͼ2������˵�����ɣ�
��ֵ��ֱ��BD��ֱ��CP�ཻ���ɵĽ�С�ǵĶ���������ͼ2������˵�����ɣ�
��3��������⣺��ͼ3��������90��ʱ������ E��F �ֱ��� CA��CB ���е㣬�� P ��FE���ӳ����ϣ�P��D��C������ͬһֱ���ϣ�AC��BD�ཻ�ڵ�M��DM��2��![]() ����AP�ij���
����AP�ij���
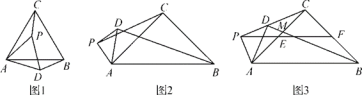
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ϵ�з���һ����OABC����֪��ABC=60����OA=1���Ƚ�����OABC��x���������������ת��ÿ�η�ת60����������ת2016�Σ���B���������ΪB1��B2��B3��������B2016������Ϊ_________��
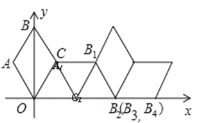
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������y��![]() ��x��0�� ����A ��3��4����ֱ��AC��x�ύ�ڵ�C ��6��0������y���ڵ�E������C��x��Ĵ���BC������������ͼ���ڵ�B��
��x��0�� ����A ��3��4����ֱ��AC��x�ύ�ڵ�C ��6��0������y���ڵ�E������C��x��Ĵ���BC������������ͼ���ڵ�B��
��1����k��ֵ��B������ꣻ
��2����ֱ��EC����ƽ�ƣ�����E�������ڷ���������ͼ���ϵĵ�E' ʱ��ֱ�߽�x���ڵ�F�����жϵ�B�Ƿ���ֱ��EF�ϲ�˵�����ɣ�
��3����ƽ�����е�M��ʹ����A��B��F��M�ĵ�Ϊ������ı���Ϊƽ���ı��Σ���ֱ��д����������������M������꣮
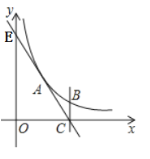
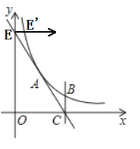
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y����x+4��������y����![]() x2+bx+c����A��B���㣬��A��y���ϣ���B��x���ϣ�
x2+bx+c����A��B���㣬��A��y���ϣ���B��x���ϣ�
��1���������ߵĽ���ʽ��
��2����x���·����������ϴ���һ��P��ʹ�á�ABP��90���������P���ꣻ
��3����E�������߶Գ�����һ�㣬��F����������һ�㣬�Ƿ���ڵ�E�͵�Fʹ���Ե�E��F��B��OΪ������ı�����ƽ���ı��Σ������ڣ������F�����ꣻ�������ڣ���˵�����ɣ�
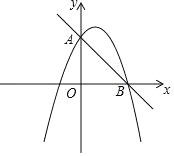
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
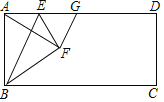
����Ŀ����ͼ���ھ���![]() �У���
����![]() ��
��![]() �ϵ�һ�����㣬����
�ϵ�һ�����㣬����![]() ������
������![]() ����
����![]() �ĶԳƵ�
�ĶԳƵ�![]() ���ҵ�
���ҵ�![]() ���ھ���
���ھ���![]() ���ڲ�������
���ڲ�������![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��
��1����֤��![]() ��
��
��2������![]() ����
����![]() ��ʱ���ú�
��ʱ���ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
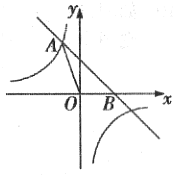
����Ŀ����ͼ��ֱ��y=��x+2�뷴��������y=![]() ��ͼ���ཻ�ڵ�A(a��3)������x���ཻ�ڵ�B��
��ͼ���ཻ�ڵ�A(a��3)������x���ཻ�ڵ�B��
��1����÷����������ı���ʽ��
��2��д��ֱ��y=��x+2����ƽ��2����λ��ֱ�߽���ʽ�����������ֱ����˫���ߵĽ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��ͼ��λ��
��ͼ��λ��![]() ���·��IJ�����
���·��IJ�����![]() �ᷭ�������Ϸ������õ����º���
�ᷭ�������Ϸ������õ����º���![]() ��ͼ��.�����º���ͼ����ֱ��
��ͼ��.�����º���ͼ����ֱ��![]() ���������㣬��
���������㣬��![]() ��ȡֵ��ΧΪ___________��
��ȡֵ��ΧΪ___________��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com