Question

已知，如图，三角形ABC是等腰直角三角形，∠ACB=90°，F是AB的中点，直线l经过点C，分别过点A、B作l的垂线，即AD⊥CE，BE⊥CE，
（1）如图1，当CE位于点F的右侧时，求证：△ADC≌△CEB；
（2）如图2，当CE位于点F的左侧时，求证：ED=BE-AD；
（3）如图3，当CE在△ABC的外部时，试猜想ED、AD、BE之间的数量关系，并证明你的猜想．

Answer 1

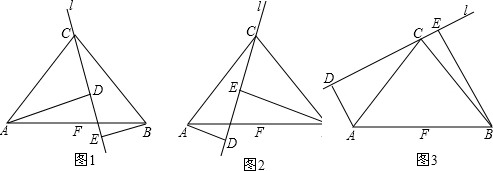
（1）证明：∵AD⊥CE，BE⊥CE，
∴∠ADC=∠CEB=90°．
∵∠ACD+∠ECB=90°，∠CAD+∠ACD=90°，
∴∠CAD=∠BCE（同角的余角相等）．
在△ADC与△CEB中
，
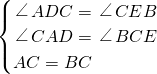
∴△ADC≌△CEB（AAS）．

（2）证明：∵AD⊥CE，BE⊥CE，
∴∠ADC=∠CEB=90°．
∵∠ACD+∠ECB=90°，∠CAD+∠ACD=90°，
∴∠CAD=∠BCE（同角的余角相等）．
在△ADC与△CEB中
，
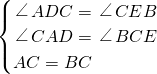
∴△ADC≌△CEB（AAS）．
∴DC=BE，AD=CE．
又∵ED=CD-CE，
∴ED=BE-AD．

（3）ED=AD+BE．
证明：∵AD⊥CE，BE⊥CE，
∴∠ADC=∠CEB=90°．
∵∠ACD+∠ECB=90°，∠CAD+∠ACD=90°，
∴∠CAD=∠BCE（同角的余角相等）．
在△ADC与△CEB中
，
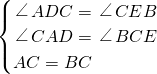
∴△ADC≌△CEB（AAS）．
∴DC=BE，AD=CE．
又∵ED=CE+DC，
∴ED=AD+BE．
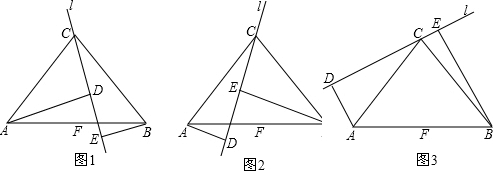
分析：（1）利用同角的余角相等得出∠CAD=∠BCE，进而根据AAS证明△ADC≌△CEB．
（2）根据AAS证明△ADC≌△CEB后，得其对应边相等，进而得到ED=BE-AD．
（3）根据AAS证明△ADC≌△CEB后，得DC=BE，AD=CE，又有ED=CE+DC，进而得到ED=AD+BE．
点评：本题考查了全等三角形的判定和性质；利用全等三角形的对应边相等进行等量交换，证明线段之间的数量关系，这是一种很重要的方法，注意掌握．