
،¾جâؤ؟،؟×غ؛دج½¾؟
زرضھإ×خïدكy£½ax2+![]() x+4µؤ¶ش³ئضلتاض±دكx£½3£¬سëxضلدཻسعA£¬Bء½µم£¨µمBشعµمAسز²à£©£¬سëyضل½»سعµمC£®
x+4µؤ¶ش³ئضلتاض±دكx£½3£¬سëxضلدཻسعA£¬Bء½µم£¨µمBشعµمAسز²à£©£¬سëyضل½»سعµمC£®
£¨1£©اَإ×خïدكµؤ½âخِت½؛حA£¬Bء½µمµؤ×ّ±ê£»
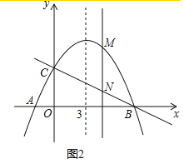
£¨2£©بçح¼1£¬بôµمPتاإ×خïدكةدB،¢Cء½µمض®¼نµؤز»¸ِ¶¯µم£¨²»سëB،¢Cضط؛د£©£¬تا·ٌ´وشعµمP£¬ت¹ثؤ±كذخPBOCµؤأو»×î´َ£؟بô´وشع£¬اَµمPµؤ×ّ±ê¼°ثؤ±كذخPBOCأو»µؤ×î´َضµ£»بô²»´وشع£¬اëثµأ÷ہيسة£»
£¨3£©بçح¼2£¬بôµمMتاإ×خïدكةدبخزâز»µم£¬¹µمM×÷yضلµؤئ½ذذدك£¬½»ض±دكBCسعµمN£¬µ±MN£½3ت±£¬ض±½سذ´³ِµمMµؤ×ّ±ê£®

،¾´ً°¸،؟£¨1£©إ×خïدكµؤ½âخِت½خھ£؛y£½©پ![]() x2+
x2+![]() x+4£»µمAµؤ×ّ±êخھ(©پ2£¬0)£¬µمBµؤ×ّ±êخھ(8£¬0)£¨2£©´وشعµمP(4£¬6)£¬ت¹µأثؤ±كذخPBOCµؤأو»×î´َ£»µمPµؤ×ّ±êخھ(4£¬6)£¬ثؤ±كذخPBOCأو»µؤ×î´َضµخھ32£¨3£©µمMµؤ×ّ±êخھ(2£¬6)،¢(6£¬4)،¢(4©پ2
x+4£»µمAµؤ×ّ±êخھ(©پ2£¬0)£¬µمBµؤ×ّ±êخھ(8£¬0)£¨2£©´وشعµمP(4£¬6)£¬ت¹µأثؤ±كذخPBOCµؤأو»×î´َ£»µمPµؤ×ّ±êخھ(4£¬6)£¬ثؤ±كذخPBOCأو»µؤ×î´َضµخھ32£¨3£©µمMµؤ×ّ±êخھ(2£¬6)،¢(6£¬4)،¢(4©پ2![]() £¬
£¬![]() ©پ1)»ٍ(4+2
©پ1)»ٍ(4+2![]() £¬©پ
£¬©پ![]() ©پ1)
©پ1)
،¾½âخِ،؟
£¨1£©¸ù¾فإ×خïدكµؤ¶ش³ئضل·½³ج£¬¼´؟ةµأµ½aµؤضµ£¬´س¶ّµأµ½؛¯ت½âخِت½£¬½ّ¶ّاَ³ِA£¬Bµؤضµ£»
£¨2£©¸ù¾ف´¶¨دµت·¨£¬اَ³ِض±دكBCµؤ½âخِت½£¬ةèµمPµؤ×ّ±êخھ£¨x£¬©پ![]() x2+
x2+![]() x+4£©£¬¹µمP×÷PD،خyضل£¬½»ض±دكBCسعµمD£¬شٍµمDµؤ×ّ±êخھ(x£¬©پ
x+4£©£¬¹µمP×÷PD،خyضل£¬½»ض±دكBCسعµمD£¬شٍµمDµؤ×ّ±êخھ(x£¬©پ![]() x+4)£¬½ّ¶ّاَ³ِPDµؤضµ£¬¸ù¾فSثؤ±كذخPBOC£½S،÷BOC+S،÷PBC£¬µأµ½¶´خ؛¯ت½âخِت½£¬¼´؟ةµأµ½´ً°¸£»
x+4)£¬½ّ¶ّاَ³ِPDµؤضµ£¬¸ù¾فSثؤ±كذخPBOC£½S،÷BOC+S،÷PBC£¬µأµ½¶´خ؛¯ت½âخِت½£¬¼´؟ةµأµ½´ً°¸£»
£¨3£©ةèµمMµؤ×ّ±êخھ(m£¬©پ![]() m2+
m2+![]() m+4)£¬شٍµمNµؤ×ّ±êخھ(m£¬©پ
m+4)£¬شٍµمNµؤ×ّ±êخھ(m£¬©پ![]() m+4)£¬شٍMN=|©پ
m+4)£¬شٍMN=|©پ![]() m2+2m |£¬¸ù¾فMN=3£¬ءذ³ِ¹طسعmµؤ·½³ج£¬¼´؟ةاَ½â£®
m2+2m |£¬¸ù¾فMN=3£¬ءذ³ِ¹طسعmµؤ·½³ج£¬¼´؟ةاَ½â£®
£¨1£©،ك إ×خïدكµؤ¶ش³ئضلتا£؛ض±دكx£½3£¬
،à ![]() £½3£¬½âµأ£؛a£½©پ
£½3£¬½âµأ£؛a£½©پ![]() £¬
£¬
،àإ×خïدكµؤ½âخِت½خھ£؛y£½©پ![]() x2+
x2+![]() x+4£®
x+4£®
µ±y£½0ت±£¬©پ![]() x2+
x2+![]() x+4£½0£¬½âµأx1£½©پ2£¬x2£½8£¬
x+4£½0£¬½âµأx1£½©پ2£¬x2£½8£¬
،àµمAµؤ×ّ±êخھ(©پ2£¬0)£¬µمBµؤ×ّ±êخھ(8£¬0)£»
£¨2£©µ±x£½0ت±£¬y£½©پ![]() x2+
x2+![]() x+4£½4£¬
x+4£½4£¬
،àµمCµؤ×ّ±êخھ(0£¬4)£®
ةèض±دكBCµؤ½âخِت½خھ£؛y£½kx+b£¨k،ظ0£©£¬
½«B(8£¬0)£¬C(0£¬4)´ْبëy£½kx+bµأ£؛![]() £¬½âµأ£؛
£¬½âµأ£؛ £¬
£¬
،àض±دكBCµؤ½âخِت½خھ£؛y£½©پ![]() x+4£®
x+4£®
¼ظةè´وشعµمP£¬ت¹ثؤ±كذخPBOCµؤأو»×î´َ£¬
ةèµمPµؤ×ّ±êخھ£¨x£¬©پ![]() x2+
x2+![]() x+4£©£¬بçح¼1£¬
x+4£©£¬بçح¼1£¬
¹µمP×÷PD،خyضل£¬½»ض±دكBCسعµمD£¬شٍµمDµؤ×ّ±êخھ(x£¬©پ![]() x+4)£¬
x+4)£¬
،àPD£½©پ![]() x2+
x2+![]() x+4©پ(©پ
x+4©پ(©پ![]() x+4)£½©پ
x+4)£½©پ![]() x2+2x£¬
x2+2x£¬
،àSثؤ±كذخPBOC£½S،÷BOC+S،÷PBC£½![]() ،ء8،ء4+
،ء8،ء4+![]() PDOB
PDOB
£½16+![]() ،ء8(©پ
،ء8(©پ![]() x2+2x)£½©پx2+8x+16
x2+2x)£½©پx2+8x+16
£½©پ£¨x©پ4£©2+32
،൱x£½4ت±£¬ثؤ±كذخPBOCµؤأو»×î´َ£¬×î´َضµتا32£®
،ك0£¼x£¼8£¬
،à´وشعµمP(4£¬6)£¬ت¹µأثؤ±كذخPBOCµؤأو»×î´َ£¬ثؤ±كذخPBOCأو»µؤ×î´َضµخھ32£®
£¨3£©ةèµمMµؤ×ّ±êخھ(m£¬©پ![]() m2+
m2+![]() m+4)£¬شٍµمNµؤ×ّ±êخھ(m£¬©پ
m+4)£¬شٍµمNµؤ×ّ±êخھ(m£¬©پ![]() m+4)£¬بçح¼2£¬
m+4)£¬بçح¼2£¬
،àMN£½|©پ![]() m2+
m2+![]() m+4©پ(©پ
m+4©پ(©پ![]() m+4)|£½|©پ
m+4)|£½|©پ![]() m2+2m |£¬
m2+2m |£¬
سض،ك MN£½3£¬
،à |©پ![]() m2+2m |£½3£¬
m2+2m |£½3£¬
µ±0£¼m£¼8ت±£¬©پ![]() m2+2m©پ3£½0£¬½âµأ£؛m1£½2£¬m2£½6£¬
m2+2m©پ3£½0£¬½âµأ£؛m1£½2£¬m2£½6£¬
،àµمMµؤ×ّ±êخھ(2£¬6)»ٍ(6£¬4)£»
µ±m£¼0»ٍm£¾8ت±£¬©پ![]() m2+2m +3£½0£¬½âµأ£؛m3£½4©پ2
m2+2m +3£½0£¬½âµأ£؛m3£½4©پ2![]() £¬m4£½4+2
£¬m4£½4+2![]() £¬
£¬
،àµمMµؤ×ّ±êخھ(4©پ2![]() £¬
£¬![]() ©پ1)»ٍ(4+2
©پ1)»ٍ(4+2![]() £¬©پ
£¬©پ![]() ©پ1)£®
©پ1)£®
´ً£؛µمMµؤ×ّ±êخھ(2£¬6£©،¢(6£¬4£©،¢(4©پ2![]() £¬
£¬![]() ©پ1£©»ٍ(4+2
©پ1£©»ٍ(4+2![]() £¬©پ
£¬©پ![]() ©پ1£©£®
©پ1£©£®




| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھ![]() تاز»صإض±½اب½اذخض½ئ¬£¬ئنضذ
تاز»صإض±½اب½اذخض½ئ¬£¬ئنضذ![]() £¬
£¬![]() £¬ذ،ءء½«ثüبئµم
£¬ذ،ءء½«ثüبئµم![]() ؤوت±صëذ×ھ؛َ
ؤوت±صëذ×ھ؛َ![]() µأµ½
µأµ½![]() £¬
£¬![]() ½»ض±دك
½»ض±دك![]() سعµم
سعµم![]() .
.

£¨1£©بçح¼1£¬µ±![]() ت±£¬
ت±£¬![]() ثùشعض±دكسëدك¶خ
ثùشعض±دكسëدك¶خ![]() سذشُرùµؤخ»ضأ¹طدµ£؟اëثµأ÷ہيسة.
سذشُرùµؤخ»ضأ¹طدµ£؟اëثµأ÷ہيسة.
£¨2£©بçح¼2£¬µ±![]() £¬اَ
£¬اَ![]() خھµبرüب½اذخت±µؤ¶بت.
خھµبرüب½اذخت±µؤ¶بت.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬،ر![]() خھ
خھ![]() µؤحâ½سش²£¬
µؤحâ½سش²£¬![]() £¬¹µم
£¬¹µم![]() µؤاذدكسë
µؤاذدكسë![]() µؤرس³¤دك½»سعµم
µؤرس³¤دك½»سعµم![]() £¬
£¬![]() ½»
½»![]() سعµم
سعµم![]() £¬
£¬![]() .
.

£¨1£©إذ¶د![]() سë
سë![]() µؤخ»ضأ¹طدµ£¬²¢ثµأ÷ہيسة£»
µؤخ»ضأ¹طدµ£¬²¢ثµأ÷ہيسة£»
£¨2£©بô![]() £¬اَ
£¬اَ![]() µؤ³¤.
µؤ³¤.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬شعئ½أوض±½ا×ّ±êدµضذ£¬سذز»¸ِ![]() £¬¶¥µمµؤ×ّ±ê·ض±ًتا
£¬¶¥µمµؤ×ّ±ê·ض±ًتا![]() .½«
.½«![]() بئشµم
بئشµم![]() ث³ت±صëذ×ھ90،مµأµ½
ث³ت±صëذ×ھ90،مµأµ½![]() £¬اëشعئ½أوض±½ا×ّ±êدµضذ×÷³ِ
£¬اëشعئ½أوض±½ا×ّ±êدµضذ×÷³ِ![]() £¬²¢ذ´³ِ
£¬²¢ذ´³ِ![]() µؤ¶¥µم×ّ±ê.
µؤ¶¥µم×ّ±ê.

²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟شع![]() ضذ£¬
ضذ£¬![]() £®
£®
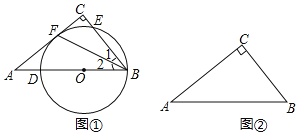
£¨1£©بçح¼¢ظ£¬µم![]() شعذ±±ك
شعذ±±ك![]() ةد£¬زشµم
ةد£¬زشµم![]() خھش²ذؤ£¬
خھش²ذؤ£¬![]() ³¤خھ°ë¾¶µؤش²½»
³¤خھ°ë¾¶µؤش²½»![]() سعµم
سعµم![]() £¬½»
£¬½»![]() سعµم
سعµم![]() £¬سë±ك
£¬سë±ك![]() دàاذسعµم
دàاذسعµم![]() £®اَض¤£؛
£®اَض¤£؛![]() £»
£»
£¨2£©شعح¼¢عضذ×÷![]() £¬ت¹ثüآْ×مزشدآجُ¼£؛
£¬ت¹ثüآْ×مزشدآجُ¼£؛
¢ظش²ذؤشع±ك![]() ةد£»¢ع¾¹µم
ةد£»¢ع¾¹µم![]() £»¢غسë±ك
£»¢غسë±ك![]() دàاذ£®
دàاذ£®
£¨³ك¹و×÷ح¼£¬ض»±£ءô×÷ح¼؛غ¼££¬²»زھاَذ´³ِ×÷·¨£©
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬ض±دك![]() µؤ½âخِ±ي´ïت½خھ
µؤ½âخِ±ي´ïت½خھ![]() £¬از
£¬از![]() سë
سë![]() ضل½»سعµم
ضل½»سعµم![]() £¬ض±دك
£¬ض±دك![]() ¾¹µم
¾¹µم![]() £¬ض±دك
£¬ض±دك![]() £¬
£¬![]() ½»سعµم
½»سعµم![]() £®
£®
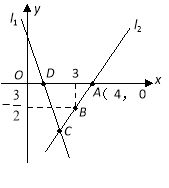
£¨1£©اَµم![]() µؤ×ّ±ê£»
µؤ×ّ±ê£»
£¨2£©اَض±دك![]() µؤ½âخِ±ي´ïت½£»
µؤ½âخِ±ي´ïت½£»
£¨3£©اَ![]() µؤأو»،£
µؤأو»،£
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬ذ،ثخ×÷³ِءث±ك³¤خھ2µؤµعز»¸ِص·½ذخA1B1C1D1£¬ثم³ِءثثüµؤأو»£®ب»؛َ·ض±ًب،ص·½ذخA1B1C1D1ثؤ±كµؤضذµمA2،¢B2،¢C2،¢D2×÷³ِءثµع¶¸ِص·½ذخA2B2C2D2£¬ثم³ِءثثüµؤأو»£®سأح¬رùµؤ·½·¨£¬×÷³ِءثµعب¸ِص·½ذخA3B3C3D3£¬ثم³ِءثثüµؤأو»،£¬سة´ث؟ةµأ£¬µعءù¸ِص·½ذخA6B6C6D6µؤأو»تا£¨،،،،£©

A. B.
B. C.
C. D.
D.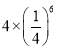
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ؤ³ضذر§ر،°خز»أûاàؤêض¾ش¸صك£؛¾±تتش،¢أوتش£¬½ل¹ûذ،أ÷؛حذ،ہِ²¢ءذµعز»£®ئہخ¯»ل¾ِ¶¨ح¨¹×¥اٍہ´ب·¶¨بثر،£®¹وشٍبçدآ£؛شع²»ح¸أ÷µؤ²¼´üہï×°سذ³رصة«ض®حâ¾ùدàح¬µؤ2¸ِ؛ىاٍ؛ح1¸ِآجاٍ£¬ذ،أ÷دبب،³ِز»¸ِاٍ£¬¼ا×،رصة«؛َ·إ»ط£¬ب»؛َذ،ہِشظب،³ِز»¸ِاٍ£®بôء½´خب،³ِµؤاٍ¶¼تا؛ىاٍ£¬شٍذ،أ÷ت¤³ِ£»بôء½´خب،³ِµؤاٍتاز»؛ىز»آج£¬شٍذ،ہِت¤³ِ£®ؤمبدخھصâ¸ِ¹وشٍ¶شث«·½¹«ئ½آً£؟اëسأءذ±ي·¨»ٍ»ت÷×´ح¼µؤ·½·¨½ّذذ·ضخِ£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬شع،÷ABCضذ£¬DE،خBC£¬EF،خAB£®
£¨1£©اَض¤£؛،÷ADE،×،÷EFC£»
£¨2£©بç¹ûAB=6£¬AD=4£¬اَ![]() µؤضµ.
µؤضµ.

²é؟´´ً°¸؛ح½âخِ>>
°ظ¶بضآذإ - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com