
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
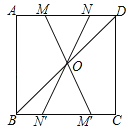
A.2对 B.3对 C.4对 D.5对
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于0.000 002 5米的颗粒物,将0.000 002 5用科学记数法表示为( )
A.0.25×10﹣5
B.2.5×10﹣5
C.2.5×10﹣6
D.2.5×10﹣7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知13 = 1 =![]() ×12×22, 13+23=9=
×12×22, 13+23=9=![]() ×22×32,13 + 23 + 33 = 36 =
×22×32,13 + 23 + 33 = 36 =![]() ×32×42, …,按照这个规律完成下列问题:
×32×42, …,按照这个规律完成下列问题:
(1)13+23+33+43+53=________=![]() × ( )2 × ( )2
× ( )2 × ( )2
(2)猜想:13+23+33+…+n3=___________
(3)利用(2)中的结论计算:(写出计算过程)
113+123 + 313+143 + 153+163 + ……+393+403.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与y轴交于点A,与x轴交于点B,且∠BAO=30°,现将△OAB沿直线AB翻折,得到△CAB. 连接OC交AB于点D.
(1)求证:AD⊥OC,OD=![]() OA ;
OA ;
(2)若Rt△AOB的斜边AB=![]() ,则OB=_____;OA=_____;点C的坐标为_______;
,则OB=_____;OA=_____;点C的坐标为_______;
(3)在(2)的条件下,动点F从点O出发,以2个单位长度/秒的速度沿折线O﹣A﹣C向终点C运动,设△FOB的面积为S(S>0),点F的运动时间为t秒,求S与t的关系式,并直接写出t的取值范围;
(4)在(3)的条件下,过点B作BE⊥x轴,交AC于点E,在动点F的运动过程中,当t为何值时,△BEF是以BE为腰的等腰三角形?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com