
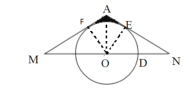
【题目】如图,△AMN为等腰三角形,点O是底边MN的中点,腰AN与⊙O相切于点E,ON与⊙O相交于点D.
(1)求证:AM与⊙O相切;
(2)若EN=![]() ,DN=2.求阴影部分的面积.
,DN=2.求阴影部分的面积.

【答案】(1)证明见解析;(2) ![]()
【解析】
(1)作辅助线证明△AOM≌△AON,即可解题,(2)利用S阴影=S△AMN-S△OEN- S△MFO - S扇形OEF即可解题.
解:(1)连接OA,OE,过点O作OF⊥AM与F,
∵△AMN为等腰三角形,点O是底边MN的中点,
∴AM=AN,OM=ON,
∴△AOM≌△AON(SSS),
∴OE=OF,
∵腰AN与⊙O相切于点E,
∴AM与⊙O相切,
(2)∵EN=![]() ,DN=2,
,DN=2,
设圆O半径=r,
∴r2+(![]() )2=(r+2)2,解得:r=2,
)2=(r+2)2,解得:r=2,
∴OE=2,ON=4,
∴∠N=30°,OA=tan30°ON=![]() ,
,
S△AMN=![]() ,
,
S△OEN=S△MFO=![]() ,
,
S扇形OEF=![]() =
=![]() ,
,
∴S阴影=![]() =
=![]() .
.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:初中数学 来源: 题型:
【题目】已知点A(2,﹣3)在双曲线y=![]() 上,则下列哪个点也在此双曲线上( )
上,则下列哪个点也在此双曲线上( )
A. (1,6) B. (﹣1,6) C. (2,3) D. (﹣2,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
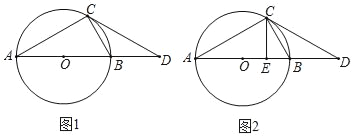
【题目】如图(1),在△ABC中,∠ACB=90°,以AB为直径作⊙O;过点C作直线CD交AB的延长线于点D,且BD=OB,CD=CA.
(1)求证:CD是⊙O的切线.
(2)如图(2),过点C作CE⊥AB于点E,若⊙O的半径为8,∠A=30°,求线段BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
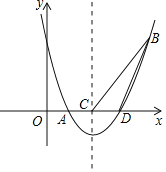
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A,D两点,并经过B点,对称轴交x轴于点C,连接BD,BC,已知A点坐标是(2,0),B点的坐标是(8,6)
x2+bx+c的图象交x轴于A,D两点,并经过B点,对称轴交x轴于点C,连接BD,BC,已知A点坐标是(2,0),B点的坐标是(8,6)
(1)求二次函数的解析式.
(2)求该函数图象的顶点坐标及D点的坐标.
(3)抛物线上有一个动点P,与A,D两点构成△ADP,是否存在S△ADP=![]() S△BCD?若存在,直接写出所有符合条件的点P的坐标;若不存在.请说明理由.
S△BCD?若存在,直接写出所有符合条件的点P的坐标;若不存在.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆柱体的体积不变,当它的高h=12.5cm时,底面积S=20cm2.
(1)求S与h之间的函数解析式;
(2)画出函数图象;
(3)当圆柱体的高为5cm,7cm时,比较底面积S的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
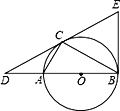
【题目】已知△ABC内接于以AB为直径的⊙O,过点C作⊙O的切线交BA的延长线于点D,且DA∶AB=1∶2.
(1)求∠CDB的度数;
(2)在切线DC上截取CE=CD,连接EB,判断直线EB与⊙O的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
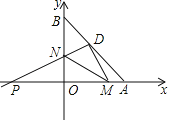
【题目】在平面直角坐标系中,点A和点B分别在x轴的正半轴和y轴的正半轴上,且OA=6,OB=8,点D是AB的中点.
(1)直接写出点D的坐标及AB的长;
(2)若直角∠NDM绕点D旋转,射线DP分别交x轴、y轴于点P、N,射线DM交x轴于点M,连接MN.
①当点P和点N分别在x轴的负半轴和y轴的正半轴时,若△PDM∽△MON,求点N的坐标;
②在直角∠NDM绕点D旋转的过程中,∠DMN的大小是否会发生变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分,每小题4分)
袋子中装有2个红球,1个黄球,它们除颜色外其余都相同。小明和小英做摸球游戏,约定一次游戏规则是:小英先从袋中任意摸出1个球记下颜色后放回,小明再从袋中摸出1个球记下颜色后放回,如果两人摸到的球的颜色相同,小英赢,否则小明赢.
(1)请用树状图或列表格法表示一次游戏中所有可能出现的结果;
(2)这个游戏规则对双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) |
|
销售玩具获得利润w(元) |
|
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com