
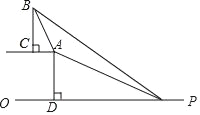
【题目】已知,如图,在坡顶A处的同一水平面上有一座大型纪念碑BC,某同学在斜坡底P处测得该碑的碑顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米到达坡顶A,在坡顶A处又测得该碑的碑顶B的仰角为76°,求纪念碑BC的高度(结果精确到0.1米).(过点A作AD⊥PO,垂足为点D.坡度=AD:PD)(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
【答案】古塔BC的高度约为18.7米.
【解析】
延长BC交OP于H.在Rt△APD中解直角三角形求出AD=10.PD=24.由题意BH=PH.设BC=x.则x+10=24+DH.推出AC=DH=x﹣14.在Rt△ABC中.根据tan76°=![]() ,构建方程求出x即可.
,构建方程求出x即可.
延长BC交OP于H.

∵斜坡AP的坡度为1:2.4,
∴![]() ,
,
设AD=5k,则PD=12k,由勾股定理,得AP=13k,
∴13k=26,
解得k=2,
∴AD=10,
∵BC⊥AC,AC∥PO,
∴BH⊥PO,
∴四边形ADHC是矩形,CH=AD=10,AC=DH,
∵∠BPD=45°,
∴PH=BH,
设BC=x,则x+10=24+DH,
∴AC=DH=x﹣14,
在Rt△ABC中,tan76°=![]() ,即
,即![]() ≈4.01.
≈4.01.
解得:x≈18.7,
经检验x≈18.7是原方程的解.
答:古塔BC的高度约为18.7米.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
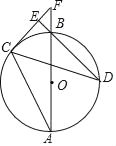
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD,过点C作CE⊥DB,垂足为E,直径AB与CE的延长线相交于F点.
(1)求证:CF是⊙O的切线;
(2)当BD=![]() ,sinF=
,sinF=![]() 时,求OF的长.
时,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
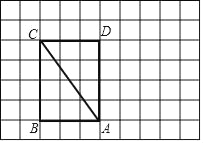
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C,D都在格点上.
(Ⅰ)AC的长为 ;
(Ⅱ)将矩形ABCD绕点A顺时针旋转得矩形AEFG,其中,点C的对应点F落在格线AD的延长线上,请用无刻度的直尺在网格中画出矩形AEFG,并简要说明点E,G的位置是如何找到的. .
查看答案和解析>>
科目:初中数学 来源: 题型:
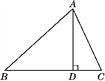
【题目】如图,在△ABC中,AD是BC边上的高,tanB=cos∠DAC.
(1)求证:AC=BD;
(2)若sin C=![]() ,BC=12,求△ABC的面积.
,BC=12,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交
轴交![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点左侧),直线
点左侧),直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,其中
两点,其中![]() 点的横坐标为2.
点的横坐标为2.
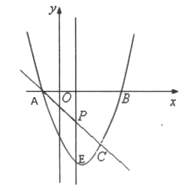
(1)求![]() 、
、![]() 两点的坐标及直线
两点的坐标及直线![]() 的函数表达式;
的函数表达式;
(2)![]() 是线段
是线段![]() 上的一个动点,过
上的一个动点,过![]() 点作
点作![]() 轴的平行线交抛物线于
轴的平行线交抛物线于![]() 点,求线段
点,求线段![]() 长度的最大值;
长度的最大值;
(3)点![]() 是抛物线上的动点,在
是抛物线上的动点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 、
、![]() 、
、![]() 、
、![]() 四个点为顶点的四边形是平行四边形?如果存在,写出所有满足条件的
四个点为顶点的四边形是平行四边形?如果存在,写出所有满足条件的![]() 点坐标(请直接写出点的坐标,不要求写过程);如果不存在,请说明理由.
点坐标(请直接写出点的坐标,不要求写过程);如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 旋转,边
旋转,边![]() 分别交边
分别交边![]() 、
、![]() 于
于![]() 、
、![]() 两点.
两点.
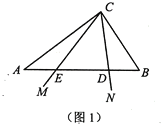

(1)若![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(2)如图2,设![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,当
,当![]() 旋转到
旋转到![]() 与
与![]() 的交点
的交点![]() 是
是![]() 的中点时,过点
的中点时,过点![]() 作
作![]() 的垂线交CM于点
的垂线交CM于点![]() ,连接
,连接![]() 、
、![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点A(-2,-8).
经过点A(-2,-8).
(1)求此抛物线的解析式;
(2)判断点B(-1,-4)是否在此抛物线上;
(3)求此抛物线上纵坐标为-6的点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
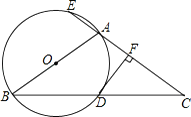
(1)试说明DF是⊙O的切线;
(2)若AC=3AE,求tanC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com