
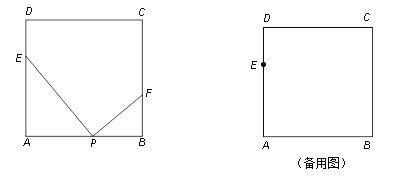
【题目】如图,在正方形ABCD中,AB=4cm,点E为AC边上一点,且AE=3cm,动点P从点A出发,以1cm/s的速度沿线段AB向终点B运动,运动时间为x s.作∠EPF=90°,与边BC相交于点F.设BF长为ycm.
(1)当x= s时,EP=PF;
(2)求在点P运动过程中,y与x之间的函数关系式;
(3)点F运动路程的长是 cm.
【答案】(1)当x=1s时,EP=PF;(2)y=﹣![]() x2+
x2+![]() x;(3)点F运动路程是
x;(3)点F运动路程是![]() cm.
cm.
【解析】
(1)利用全等三角形的性质即可解决问题;
(2)利用相似三角形的性质,即可解决问题;
(3)两条二次函数的性质,求出y的最大值即可解决问题;
(1)∵四边形ABCD是正方形,∠EPF=90°,
∴∠A=∠B=90°,
∴∠APE+∠AEP=90°,∵∠APE+∠BPF=90°,
∴∠BPF=∠AEP,∵EP=PF,
∴△AEP≌△BPF,
∴AE=PB=3,
∴AP=AB﹣PB=1,
∴当x=1s时,EP=PF;
(2)∵∠EPF=90°,
∴∠EPA+∠BPF=90°
又∵∠EPA+∠AEP=90°,
∴∠AEP=∠BPF,
在△EAP与△PBF中,
∠AEP=∠BPF,∠EAP=∠PBF=90°,
∴△EAP∽△PBF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴y=﹣![]() x2+
x2+![]() x.
x.
(3)∵y=﹣![]() x2+
x2+![]() x=﹣
x=﹣![]() (x﹣2)2+
(x﹣2)2+![]() ,
,
∵﹣![]() <0,
<0,
∴y有最大值,最大值为![]() ,
,
∴点F运动路程是![]() cm.
cm.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:初中数学 来源: 题型:
【题目】新华商场销售某种冰箱,每台进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,设每台冰箱的定价为x元,则x满足的关系式为( )
A. (x2500)(8+4×![]() )=5000 B. (2900x2500)(8+4×
)=5000 B. (2900x2500)(8+4×![]() )=5000
)=5000
C. (x2500)(8+4×![]() )=5000 D. (2900x)(8+4×
)=5000 D. (2900x)(8+4×![]() )=5000
)=5000
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y=![]() 上一点,过A作AB∥x轴,交直线y=﹣x于点B,点D是x轴上一点,连接BD交双曲线于点C,连接AD,若BC:CD=3:2,△ABD的面积为
上一点,过A作AB∥x轴,交直线y=﹣x于点B,点D是x轴上一点,连接BD交双曲线于点C,连接AD,若BC:CD=3:2,△ABD的面积为![]() ,tan∠ABD=
,tan∠ABD=![]() ,则k的值为( )
,则k的值为( )

A. ﹣2 B. ﹣3 C. ﹣![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要从甲.乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
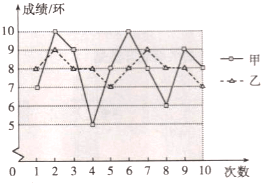
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图形,直接写出甲,乙这10次射击成绩的方差![]() ,
, ![]() 哪个大;
哪个大;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选 参赛更合适;如果其他班级参赛选手的射击成绩都在9环左右,本班应该选 参赛更合适.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 方格纸中小正方形的边长为1,
方格纸中小正方形的边长为1,![]() ,
,![]() 两点在格点上,要在图中格点上找到点
两点在格点上,要在图中格点上找到点![]() ,使得
,使得![]() 的面积为2,满足条件的点
的面积为2,满足条件的点![]() 有( )
有( )

A.无数个B.7个C.6个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
(3)在(2)的条件下,求线段BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰![]() 和等腰
和等腰![]() 中,
中,![]() ,
,![]() ,连接
,连接![]() 交于点
交于点![]() .
.
(1)如图1,若![]() :
:
①![]() 与
与![]() 的数量关系为 ;
的数量关系为 ;
②![]() 的度数为 ;
的度数为 ;
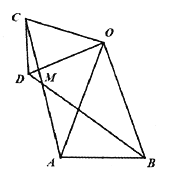
图1
(2)如图2,若![]() :
:
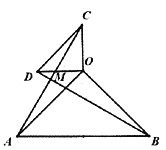
图2
①判断![]() 与
与![]() 之间存在怎样的数量关系?并说明理由;
之间存在怎样的数量关系?并说明理由;
②求![]() 的度数;
的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
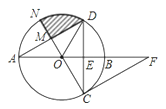
【题目】如图,AB为⊙O的直径,弦CD垂直平分OB于点E,点F在AB延长线上,∠AFC=30°.
(1)求证:CF为⊙O的切线.
(2)若半径ON⊥AD于点M,CE=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有五张正面分别写有数字﹣3,﹣2,1, 2,3的卡片,它们的背面完全相同,现将这五张卡片背面朝上洗匀后随机抽取一张,以其正面的数字作为a的值,然后再从剩余的四张卡片中随机抽取一张,以其正面的数字作为b的值,用列表法或树状图法求点(a,b)在反比例函数y=![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com