
【题目】如图,在△ABC中,AD是BC边上的高,tanC= ![]() ,AC=3
,AC=3 ![]() ,AB=4,求△ABC的周长.
,AB=4,求△ABC的周长. 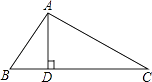
【答案】解:在Rt△ADC中,tanC= ![]() =
= ![]() , 设AD=k,CD=2k,
, 设AD=k,CD=2k,
AC= ![]() =
= ![]() k,
k,
∵AC=3 ![]() ,
,
∴ ![]() k=3
k=3 ![]() ,解得k=3,
,解得k=3,
∴AD=3,CD=6,
在Rt△ABD中,
BD= ![]() =
= ![]() =
= ![]() ,
,
∴△ABC的周长=AB+AC+BD+CD=4+3 ![]() +
+ ![]() +6=10+3
+6=10+3 ![]() +
+ ![]()
【解析】在Rt△ADC中,根据正切的定义得到tanC= ![]() =
= ![]() ,则可设AD=k,CD=2k,接着利用勾股定理得到AC=
,则可设AD=k,CD=2k,接着利用勾股定理得到AC= ![]() k,则
k,则 ![]() k=3
k=3 ![]() ,解得k=3,所以AD=3,CD=6,然后在Rt△ABD中,利用勾股定理计算出BD=
,解得k=3,所以AD=3,CD=6,然后在Rt△ABD中,利用勾股定理计算出BD= ![]() ,再根据三角形的周长的定义求解.
,再根据三角形的周长的定义求解.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注,人工智能完胜李世石.某教学网站开设了有关人工智能的课程并策划了A,B两种网上学习的月收费方式:
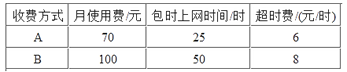
设小明每月上网学习人工智能课程的时间为x小时,方案A,B的收费金额分别为yA元、yB元.
(1)当x≥50时,分别求出yA、yB与x之间的函数表达式;
(2)若小明3月份上该网站学习的时间为60小时,则他选择哪种方式上网学习合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形纸片ABCD的边长为4,将该正方形纸片沿EF折叠(E,F分别在AB,CD边上),使点B落在AD边上的点M处,点C落在点N处,MN与CD交于点P.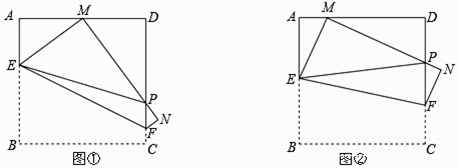
(1)如图①,连接PE,若M是AD边的中点.
①写出图中与△PMD相似的三角形.
②求△PMD的周长.
(2)如图②,随着落点M在AD边上移动(点M不与A、D重合),△PDM的周长是否发生变化?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠C=120°,AD=2AB=4,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF.则EF的最大值与最小值的差为( )

A. 1 B. ![]() ﹣1 C.
﹣1 C. ![]() D. 2﹣
D. 2﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别骑自行车和摩托车从A地到B地,两人所行驶的路程与时间的关系如图所示,下面的四个说法:
![]() 甲比乙早出发了3小时;
甲比乙早出发了3小时;![]() 乙比甲早到3小时;
乙比甲早到3小时;![]() 甲、乙的速度比是5:6;
甲、乙的速度比是5:6;![]() 乙出发2小时追上了甲.
乙出发2小时追上了甲.
其中正确的个数是![]()
![]()
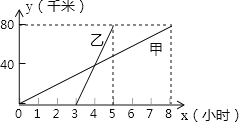
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证: 
(1)AF=CG;
(2)CF=2DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.
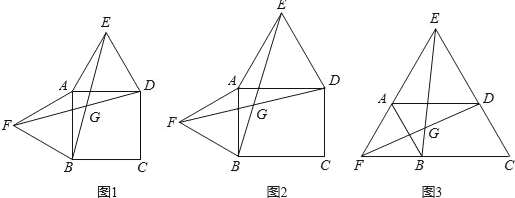
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)单项式﹣2x3ym与5xn+1y的差是一个单项式,求![]() 的值;
的值;
(2)化简求值:(x2+5﹣4x3)﹣2(﹣2x3+5x﹣4),其中x=﹣2;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com