
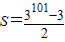
 +(
+( )2+…+(
)2+…+( )9]的值,令S=1+
)9]的值,令S=1+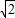 +(
+(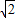 )2+…+(
)2+…+(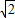 )9,根据同底数幂的乘法法则求出
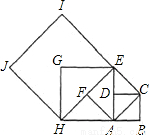
)9,根据同底数幂的乘法法则求出 S的表达式,再把两式相减即可求出S的值,从而所有的正方形的所有边长之和.
S的表达式,再把两式相减即可求出S的值,从而所有的正方形的所有边长之和.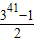 .
. +(
+(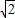 )2+…+(
)2+…+( )9],
)9], +(
+(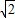 )2+…+(
)2+…+(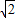 )9①、
)9①、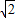 S=
S=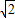 +(
+(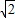 )2+…+(
)2+…+( )10②,
)10②,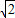 -1)S=32-1=31,S=31×(
-1)S=32-1=31,S=31×( +1).
+1). +1)=124
+1)=124 +124.
+124.

科目:初中数学 来源: 题型:阅读理解
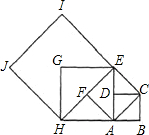 阅读下面的文字,回答后面的问题.
阅读下面的文字,回答后面的问题.| 3101-3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5101-5 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 阅读下面的文字,回答后面的问题.
阅读下面的文字,回答后面的问题.| 3101-3 |
| 2 |
| 3101-3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com