
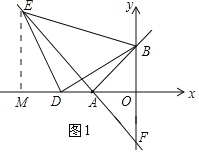
【题目】如图1,在平面直角坐标系中,直线AB与x轴交于点A(m,0),与y轴交于点B(0,n),且m,n满足:(m+n)2+|n﹣6|=0.

(1)求:①m,n的值;②S△ABO的值;
(2)D为OA延长线上一动点,以BD为直角边作等腰直角△BDE,连接EA,求直线EA与y轴交点F的坐标.
(3)如图2,点E为y轴正半轴上一点,且∠OAE=30°,AF平分∠OAE,点M是射线AF上一动点,点N是线段OA上一动点,试求OM+MN的最小值(图1与图2中点A的坐标相同).
【答案】(1)①m=﹣6,n=6,②18;(2)F(0,﹣6);(3)OM+MN的最小值为3.
【解析】
(1)①利用非负数的性质即可解决问题.
②先确定出OA=OB=6,从而求得△ABO的面积.
(2)先判断出△DEM≌△BDO得出EM=DO,MD=OB=OA=6,进而判断出AM=EM,即可得出∠OAF=45°,即可得出点F坐标,最后用待定系数法得出直线EA解析式.
(3)过点O作OG⊥AE于G,交AF于M,作MN⊥OA于N,连接MN,此时OM+MN的值最小.
(1)①∵(m+n)2+|n﹣6|=0,
又∵(m+n)2≥0,|n﹣6|≥0.
∴m+n=0,n=6,
∴m=﹣6,n=6.
②∵直线AB与x轴交于点A(﹣6,0),与y轴交于B(0,6).
∴OA=6,OB=6,
∴S△ABO=![]() OAOB=
OAOB=![]() ×6×6=18;
×6×6=18;
(2)如图1,过点E作EM⊥x轴于M,
∴∠MDE+∠DEM=90°,
∵△BDE是等腰直角三角形,
∴DE=DB,∠BDE=90°,
∴∠MDE+∠BDO=90°,
∴∠DEM=∠BDO,
在△DEM和△BDO中,
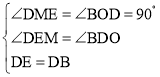 ,
,
∴△DEM≌△BDO(AAS),
∴EM=DO,MD=OB=OA=6,
∴AM=DM+AD=6+AD,
EM=OD=OA+AD=6+AD,
∴EM=AM,
∴∠MAE=45°=∠OAF,
∴OA=OF,
∴F(0,﹣6).
(3)如图2中,

过点O作OG⊥AE于G,交AF于M,作MN⊥OA于N,连接MN,此时OM+MN的值最小.
∵∠MAG=∠MAN,MG⊥AG,MN⊥AN,
∴MG=MN,
∴OM+MN=OM+MG=OG,
在Rt△OAG中,∠OAE=30°,OA=6,
∴OG=3,
∴OM+MN的最小值为3.


科目:初中数学 来源: 题型:
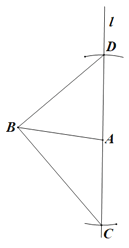
【题目】在一次研究性学习活动中,同学们看到了工人师傅在木板上画一个直角三角形的过程(如图所示):画线段AB,过点A任作一条直线l,以点A为圆心,以AB长为半径画弧,与直线l相交于两点C、D,连接BC和BD.则△BCD就是直角三角形.
(1)请你说明△BCD是直角三角形的道理;
(2)请利用上述方法作一个直角三角形,使其中一个锐角为60°(不写作法,保留作图
痕迹,在图中注明60°的角).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2的图象与一次函数y=mx+4的图象相交于点A(-2,2)和B(n,8)两点.
(1)求二次函数y=ax2与一次函数y=mx+4的表达式;
(2)试判断△AOB的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A(-2,1),B(-3,4),C(-1,3),过点(l,0)作x轴的垂线![]() .
.
(1)作出△ABC关于直线![]() 的轴对称图形△
的轴对称图形△![]() ;
;
(2)直接写出A1(___,___),B1(___,___),C1(___,___);
(3)在△ABC内有一点P(m,n),则点P关于直线![]() 的对称点P1的坐标为(___,___)(结果用含m,n的式子表示).
的对称点P1的坐标为(___,___)(结果用含m,n的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三条边都相等的三角形叫做等边三角形,它的三个角都是60°.△ABC是等边三角形,点D在BC所在直线上运动,连接AD,在AD所在直线的右侧作∠DAE=60°,交△ABC的外角∠ACF的角平分线所在直线于点E.
(1)如图1,当点D在线段BC上时,请你猜想AD与AE的大小关系,并给出证明;
(2)如图2,当点D在线段BC的反向延长线上时,依据题意补全图形,请问上述结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com