
����Ŀ�������������ν��߳�Ϊn��n��5����nΪ�������������ηָ�ΪһЩ1x5��2��3�ľ��Σ�axb �ľ���ָ�߳��ֱ�Ϊa��b�ľ��Σ���
����̽���������ȴӼ����ʼ�о�������ٰѸ�������ת��Ϊ�ѽ�������⣮
̽��һ��
��ͼ�٣���n=5ʱ���ɽ������ηָ�Ϊ���1��5�ľ��Σ�
��ͼ�ڣ���n=6ʱ���ɽ������ηָ�Ϊ����2��3�ľ��Σ�
��ͼ�ۣ���n=7ʱ���ɽ������ηָ�Ϊ���1��5�ľ��κ��ĸ�2��3�ľ���
��ͼ�ܣ���n=8ʱ���ɽ������ηָ�Ϊ�˸�1��5�ľ��κ��ĸ�2��3�ľ���
��ͼ�ݣ���n=9ʱ���ɽ������ηָ�Ϊ�Ÿ�1��5�ľ��κ�����2��3�ľ���

̽������
��n=10��11��12��13��14ʱ���ֱ������ΰ����з�ʽ�ָ

���ԣ���n=10��11��12��13��14ʱ�����ɽ������ηָ�Ϊһ��5��5�������Ρ�һ����n��5 ������ n��5 ���������κ�����5����n��5���ľ��Σ���Ȼ��5��5�������κ�5����n��5���ľ��ξ��ɷָ�Ϊ1��5�ľ��Σ�����n��5������n��5�����������DZ߳��ֱ�Ϊ5��6��7��8��9 �������Σ���̽��һ�ķ����ɷָ�ΪһЩ1��5��2��3�ľ��Σ�
̽������
��n=15��16��17��18��19ʱ���ֱ������ΰ����з�ʽ�ָ

�밴������ķ������ֱ��߳�Ϊ18��19�������ηָ�ʾ��ͼ��
���ԣ���n=15��16��17��18��19ʱ�����ɽ������ηָ�Ϊһ��10��10�������Ρ�һ����n��10 ������n��10���������κ�����10����n��10���ľ��Σ���Ȼ��10��10�������κ�10����n��10���ľ��ξ��ɷָ�Ϊ1x5�ľ��Σ�����n��10������n��10�������������DZ߳��ֱ�Ϊ5��6��7��8��9�������Σ���̽��һ�ķ����ɷָ�ΪһЩ1��5��2��3�ľ��Σ�
����������ν��߳�Ϊn��n��5����nΪ�������������ηָ�ΪһЩ1��5��2��3�ľ��Σ��밴������ķ��������ָ�ʾ��ͼ��������˵����
ʵ��Ӧ�ã���ν��߳�Ϊ61�������ηָ�ΪһЩ1��5��2��3�ľ��Σ���ֻ�谴��̽�����ķ��������ָ�ʾ��ͼ���ɣ�
���𰸡�̽�������𰸼����������������𰸼�������ʵ��Ӧ�ã��𰸼�������
��������
����������ȴӼ����ʼ�о�������ٰѸ�������ת��Ϊ�ѽ�������⣬�ɴ˰�Ҫ�������ת��Ϊ�Ѿ���������⣬���ɽ�����⣮
���������̽�������߳�Ϊ18��19�������ηָ�ʾ��ͼ����ͼ��ʾ��
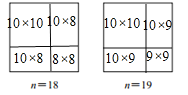
����������5��n��10ʱ����̽��һ��
��n��10����n=5a+b������a��bΪ��������5��b��10����ͼ����ͼ��ʾ�����ɽ������ηָ�Ϊһ��5a��5a�������Ρ�һ��b��b�������κ�����5a��b�ľ��Σ���Ȼ��5a��5a�������κ�5a��b�ľ��ξ��ɷָ�Ϊ1x5�ľ��Σ���b��b�����������DZ߳��ֱ�Ϊ5��6��7��8��9�������Σ���̽��һ�ķ����ɷָ�ΪһЩ1��5��2��3�ľ��μ��ɣ�
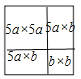
���������߳�Ϊ61�������ηָ�ΪһЩ1��5��2��3�ľ��Σ���ͼ��ʾ��
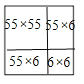



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����BAC=120�㣬AE=BE��DΪEC�е㣮 
��1�����CAE�Ķ�����
��2����֤����ADE�ǵȱ������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��2016����ͼ1��һ�κ���y=kx��3��k��0����ͼ����y�ύ�ڵ�A���뷴��������![]() ��x��0����ͼ���ڵ�B��4��b����
��x��0����ͼ���ڵ�B��4��b����
��1��b= ��k= ��
��2����C���߶�AB�ϵĶ��㣨�ڵ�A��B���غϣ�������C��ƽ����y���ֱ��l�����������������ͼ���ڵ�D������OCD��������ֵ��
��3������2�������ȡ�����ֵ����OCD������AB����ƽ��һ���ľ��룬�õ���O��C��D�䣬����O�Ķ�Ӧ��O�����ڸ÷���������ͼ���ϣ���ͼ2�������D��������� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������һ���ϵĸ���������һ�룬��������������εĵ��ǣ� ��
A.75���15��
B.75��
C.15��
D.75���30��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���B=46�㣬��C=54�㣬ADƽ�֡�BAC����BC��D��DE��AB����AC��E�����ADE�Ĵ�С�ǣ� �� 
A.45��
B.54��
C.40��
D.50��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¼��У���ȷ���¼����ǣ�������
A.�����˶�Ա���߶���1.80������
B.�ܵܵ�����һ���ȸ�����
C.����ͼ����ⴥ��
D.�����к����彡��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���A=90�㣬DE��BC�Ĵ�ֱƽ���ߣ�AD=DE�����C�Ķ������㣮 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��AD=AE��BD=CE����ADB=AEC=100�㣬��BAE=70�㣬���н��۴�����ǣ� �� 
A.��ABE�ա�ACD
B.��ABD�ա�ACE
C.��C=30��
D.��DAE=40��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com