若∠A.∠B是直角三角形ABC的两个锐角.则关于x的方程tgA•x2-4x+tgB=0的根的情况为有两个不相等实根．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

20、若∠A、∠B是直角三角形ABC的两个锐角，则关于x的方程tgA•x²-4x+tgB=0的根的情况为

有两个不相等实根

．

分析：先表示出△，然后利用互余两个角的正切互为倒数计算出△的值，最后进行判断根的情况．

解答：解：由于∠A，∠B是Rt△ABC的两个锐角，则∠B=90°-∠A，
因为tgA≠0，得△=4²-4tgA•tgB=16-4tgA•ctgA=16-4=12＞0，
所以方程有两个不相等的实数根．
故答案为有两个不相等的实数根．

点评：本题考查了一元二次方程ax²+bx+c=0（a≠0，a，b，c为常数）根的判别式．当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．同时考查了互余两个角的正切互为倒数．

练习册系列答案

中学生英语随堂演练及单元要点检测题系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

如图，在梯形ABCD中，AD∥BC，AB=DC，AD=6，BC=12，梯形ABCD的面积为36，动点P从D点出发沿DC以每秒1个单位的速度向终点C运动，动点Q从C点出发沿CB以每秒2个单位的速

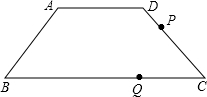度向点B运动，两点同时出发，点P到达点C时，Q点随之停止运动．
（1）线段CD的长为

；
（2）设P、Q运动时间为t（0＜t＜5）秒，PQ与梯形ABCD的边DC、BC所围成的三角形的面积为S，求S与t之间的函数关系式；
（3）是否存在某一时刻，使以P、Q、C三点为顶点的三角形是直角三角形，若有，请求出相应时间；若没有，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

已知：△AOC如图A（-1，0）、C（0，3），把△AOC 以O点为旋转中心顺时针方向旋转
90°，使C与B重合
（1）写出B点的坐标，求经过A、B、C三点的抛物线的解析式并画出图象；
（2）求抛物线顶点D的坐标，求证：△BCD是直角三角形；
（3）我们知道△DBC是直角三角形，在抛物线上除D点外，是否还存在另外一个点P，使得△PBC是直角三角形？若存在，请用尺规作图画出这样的点；若不存在，请说明理由；
（4）设抛物线的对称轴与x轴交于点H，射线CH交以O为圆心OC为半径的圆于G，求HG的长．

查看答案和解析>>

科目：初中数学 来源：新教材完全解读　九年级数学　(下册)　(配华东师大版新课标) 华东师大版新课标 题型：013

下列叙述中，正确的是

[　　]

A．直角三角形中，两条边的平方和等于第三边的平方

B．如果一个三角形中两边的平方差等于第三边的平方，那么这个三角形是直角三

角形

C．△ABC中，∠A，∠B，∠C的对边分别是a，b，c，若c²－a²＝b²，则∠B＝90°

D．若三角形三个内角之比是3∶4∶5，则该三角形为直角三角形

查看答案和解析>>

科目：初中数学 来源： 题型：

我们知道,只有两边和一角对应相等的两个三角形不一定全等.你如何处理和安排这三个条件,使这两个三角形全等.请你仿照方案(1),写出方案(2)、(3).