
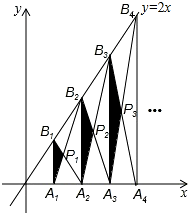
 ČēĶ¼£¬ŅŃÖŖA1”¢A2”¢A3”¢””¢An”¢An+1ŹĒxÖįÉĻµÄµć£¬ĒŅOA1=A1A2=A2A3=”=AnAn+1=1£¬·Ö±š¹żµćA1”¢A2”¢A3”¢””¢An”¢An+1×÷xÖįµÄ“¹Ļß½»Ö±Ļßy=2xÓŚµćB1”¢B2”¢B3”¢””¢Bn”¢Bn+1£¬Į¬½ÓA1B2”¢B1A2”¢A2B3”¢B2A3”¢””¢AnBn+1”¢BnAn+1£¬ŅĄ“ĪĻą½»ÓŚµćP1”¢P2”¢P3”¢””¢Pn£®”÷A1B1P1”¢”÷A2B2P2”¢”÷AnBnPnµÄĆ껿ŅĄ“Ī¼ĒĪŖS1”¢S2”¢S3”¢””¢Sn£¬ŌņSnĪŖ£Ø””””£©
ČēĶ¼£¬ŅŃÖŖA1”¢A2”¢A3”¢””¢An”¢An+1ŹĒxÖįÉĻµÄµć£¬ĒŅOA1=A1A2=A2A3=”=AnAn+1=1£¬·Ö±š¹żµćA1”¢A2”¢A3”¢””¢An”¢An+1×÷xÖįµÄ“¹Ļß½»Ö±Ļßy=2xÓŚµćB1”¢B2”¢B3”¢””¢Bn”¢Bn+1£¬Į¬½ÓA1B2”¢B1A2”¢A2B3”¢B2A3”¢””¢AnBn+1”¢BnAn+1£¬ŅĄ“ĪĻą½»ÓŚµćP1”¢P2”¢P3”¢””¢Pn£®”÷A1B1P1”¢”÷A2B2P2”¢”÷AnBnPnµÄĆ껿ŅĄ“Ī¼ĒĪŖS1”¢S2”¢S3”¢””¢Sn£¬ŌņSnĪŖ£Ø””””£©A”¢
| ||
BӢ
| ||
CӢ
| ||
DӢ
|
 “ŗÓź½ĢÓżĶ¬²½×÷ĪÄĻµĮŠ“š°ø
“ŗÓź½ĢÓżĶ¬²½×÷ĪÄĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ČēĶ¼1£¬ŌŚRt”÷ABCÖŠ£¬”ĻACB=90”ć£¬µćPŅŌĆæĆė2cmµÄĖŁ¶Č“ÓµćA³ö·¢£¬ŃŲÕŪĻßAC-CBŌĖ¶Æ£¬µ½µćBĶ£Ö¹£®¹żµćP×÷PD”ĶAB£¬“¹×ćĪŖD£¬PDµÄ³¤y£Øcm£©ÓėµćPµÄŌĖ¶ÆŹ±¼äx£ØĆė£©µÄŗÆŹżĶ¼ĻóČēĶ¼2£®µ±µćPŌĖ¶Æ5ĆėŹ±£¬PDµÄ³¤ŹĒ£Ø””””£©
ČēĶ¼1£¬ŌŚRt”÷ABCÖŠ£¬”ĻACB=90”ć£¬µćPŅŌĆæĆė2cmµÄĖŁ¶Č“ÓµćA³ö·¢£¬ŃŲÕŪĻßAC-CBŌĖ¶Æ£¬µ½µćBĶ£Ö¹£®¹żµćP×÷PD”ĶAB£¬“¹×ćĪŖD£¬PDµÄ³¤y£Øcm£©ÓėµćPµÄŌĖ¶ÆŹ±¼äx£ØĆė£©µÄŗÆŹżĶ¼ĻóČēĶ¼2£®µ±µćPŌĖ¶Æ5ĆėŹ±£¬PDµÄ³¤ŹĒ£Ø””””£©| A”¢1.2cm | B”¢1.6cm | C”¢2cm | D”¢2.4cm |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| A”¢µŚ¶ž”¢Čż”¢ĖÄĻóĻŽ | B”¢µŚŅ»”¢¶ž”¢ČżĻóĻŽ | C”¢µŚŅ»”¢Čż”¢ĖÄĻóĻŽ | D”¢µŚŅ»”¢¶ž”¢ĖÄĻóĻŽ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ¶ž“ĪŗÆŹży=a£Øx+h£©2+kµÄĶ¼ĻóČēĶ¼£¬ŌņŅ»“ĪŗÆŹży=hx+kµÄĶ¼Ļó²»¾¹żµÄĻóĻŽŹĒ£Ø””””£©
¶ž“ĪŗÆŹży=a£Øx+h£©2+kµÄĶ¼ĻóČēĶ¼£¬ŌņŅ»“ĪŗÆŹży=hx+kµÄĶ¼Ļó²»¾¹żµÄĻóĻŽŹĒ£Ø””””£©| A”¢µŚŅ»ĻóĻŽ | B”¢µŚ¶žĻóĻŽ | C”¢µŚČżĻóĻŽ | D”¢µŚĖÄĻóĻŽ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| A”¢£Ø1£¬2£© | B”¢£Ø-2£¬-1£© | C”¢£Ø-1£¬2£© | D”¢£Ø2£¬-4£© |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| A”¢y1£¾y2£¾y3 | B”¢y3£¾y2£¾y1 | C”¢y1£¾y3£¾y2 | D”¢y3£¾y1£¾y2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| AӢ-10 | BӢ-6 | CӢ10 | DӢ14 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ČēĶ¼£¬Ö±Ļßy1=x+bÓėy2=kx-1Ļą½»ÓŚµćP£¬µćPµÄŗį×ų±źĪŖ-1£¬Ōņ¹ŲÓŚxµÄ²»µČŹ½x+b£¾kx-1µÄ½ā¼ÆŌŚŹżÖįÉĻ±ķŹ¾ÕżČ·µÄŹĒ£Ø””””£©
ČēĶ¼£¬Ö±Ļßy1=x+bÓėy2=kx-1Ļą½»ÓŚµćP£¬µćPµÄŗį×ų±źĪŖ-1£¬Ōņ¹ŲÓŚxµÄ²»µČŹ½x+b£¾kx-1µÄ½ā¼ÆŌŚŹżÖįÉĻ±ķŹ¾ÕżČ·µÄŹĒ£Ø””””£©A”¢ | B”¢ | C”¢ | D”¢ |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com