已知:抛物线y=ax2+2x+c,对称轴为直线x=-1,抛物线与y轴交于点C,与x轴交于A(-3,0)、B两点.
(1)求直线AC的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)P为抛物线上一点,若以线段PB为直径的圆与直线BC切于点B,求点P的坐标.
分析:(1)由对称轴为直线x=-1,与x轴交于A(-3,0)、B两点,求出a的值与B点的坐标,进而求出C点的坐标,再求出直线AC的解析式;
(2)将四边形ABCD面积用同一未知数表示,求出二次函数的最值即可,
(3)以线段PB为直径的圆与直线BC切于点B,作出图形,由三角形相似求出P点的坐标.
解答:解:(1)∵对称轴
x=-=-1∴a=1∵A(-3,0)∴c=-3
设直线AC的解析式为y=kx+b
∵A(-3,0),C(0,-3),代入得:
直线AC的解析式为y=-x-3
(2)代数方法一:
过点D作DM∥y轴分别交线段AC和x轴于点M、N.
设D(x,x
2+2x-3),则M(x,-x-3)
∵S
四边形ABCD=S
△ABC+S
△ACD
=
6+×DM×(AN+ON)=6+DM=
6+[(-x-3)=
-x2-x+6=
-(x+)2+∴当
x=-时,四边形ABCD面积有最大值
.
代数方法二:S
四边形ADCB=S
△ADN+S
梯形NDCO+S
△OBC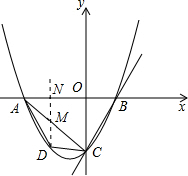
=
(x+3)(-x2-2x+3)+(-x2-2x+3+3)(-x)+=
-x2-x+6=-(x+)2+∴当
x=-时,四边形ABCD面积有最大值
.
几何方法:
过点D作AC的平行线l,设直线l的解析式为y=-x+b.
由
得:x
2+3x-b-3=0
当△=3
2-4(-b-3)=0时,直线l与抛物线只有一个公共点
即:当
b=-时,△ADC的面积最大,四边形ABCD面积最大
此时公共点D的坐标为
(-,-)S
四边形ADCB=S
△ADN+S
梯形NDCO+S
△OBC
| | =AN•DN+(DN+OC)ON+OB•OC | | =OA•DN+OC•ON+OB•OC | | =×3×+×3×+×1×3 |
| |
=
即:当
x=-时,四边形ABCD面积有最大值
.
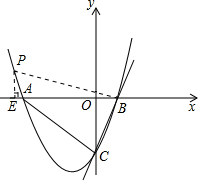
(3)如图所示,因为A(-3,0),抛物线对称轴为直线x=-1,
由抛物线的轴对称性可求得B(1,0),
∵以线段PB为直径的圆与直线BC切于点B,
∴过点B作BC的垂线交抛物线于一点,则此点必为点P.
过点P作PE⊥x轴于点E,
∵A(-3,0),C(0,-3),
∴PB=BC,PE=OB,
∴Rt△PEB∽Rt△BOC
∴
=,故EB=3PE,
设P(x,x
2+2x-3),∵B(1,0)
∴BE=1-x,PE=x
2+2x-3,则1-x=3(x
2+2x-3),
解得x
1=1(不合题意舍去),
x2=-,
∴P点的坐标为:
(-,).
点评:此题主要考查了二次函数的对称性,以及二次函数的最值问题和相似三角形的判定.





 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
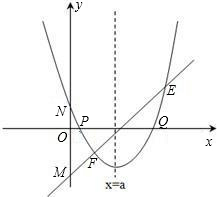
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. (2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.
(2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.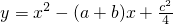 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边. ,抛物线与x轴交于点P、Q,问是否
,抛物线与x轴交于点P、Q,问是否 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边. ,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.