练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，△ABC内有一点O，且OA=OB=OC，若∠OAB=20°，∠OAC=30°，则∠BOC=（　　）
    分析：根据等腰三角形的性质得出∠OAB=∠OBA=20°，∠OAC=∠OCA=30°，在△ABC中，根据三角形内角和定理得出∠OAB+∠OBA+∠OAC+∠OCA+∠OCB+∠OBC=180°，代入求出∠OCB+∠OBC的度数，进一步求出∠BOC的度数即可．
    解答：解：∵OA=OB=OC，∠OAB=20°，∠OAC=30°，
    ∴∠OAB=∠OBA=20°，∠OAC=∠OCA=30°，
    在△ABC中，∠OCB+∠OBC=180°-20°×2-30°×2=80°，
    ∴∠BOC=180°-80°=100°．
    故选：D．
    点评：本题考查了三角形内角和定理和等腰三角形的性质的应用，主要考查学生的计算和推理能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2012•如东县一模）如图，在平面直角坐标系中，小方格都是边长为1的正方形，△ABC的顶点A、B、C都在格点上，其中A点坐标为（-2，3）．请你解答下列问题：
    （1）将△ABC沿x轴翻折后再沿x轴向右平移3个单位，在图中画出平移后的图形，经过两次变换后A点坐标变为
    （1，-3）
    （1，-3）
    ；
    （2）在问题（1）中，若△ABC内有一点P（a，b），则经过两次变换后点P坐标变为
    （a+3，-b）
    （a+3，-b）
    ；
    （3）如图，△A′B′C′是△ABC绕某点逆时针旋转90°后的图形，则旋转中心的坐标为
    （1，2）
    （1，2）
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•玄武区一模）如图，△ABC内接于⊙O，∠DAB=∠ACB．
    （1）判断直线AD与⊙O的位置关系，并说明理由；
    （2）若∠DAB=30°，AB=1，求弦AB所对的弧长；
    （3）在（2）的条件下，点C在优弧AB上运动，是否存在点C，使点O到弦BC的距离为
    12
    ？若有，请直接写出AC的长；若没有，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

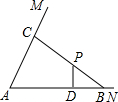    精英家教网如图，在∠MAN内有一定点P，已知tan∠MAN=3，P到直线AN的距离PD=12，AD=30．过P任作一条直线分别与AN、AM交于点B、C．求△ABC面积的最小值．

    查看答案和解析>>

    科目：初中数学 来源：黄冈难点课课练　　八年级数学上册 题型：013

    如图，△ABC内有D、E、F、G四个点，分别以A、B、C、D、E、F、G(任意三点不在一直线上)七个点为顶点画三角形，如果每个三角形的顶点不在另一个三角形的内部，那么这些三角形的所有内角之和为

    [　　]

    A．
    B．
    C．
    D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    如图，在△ABC内有一矩形，D在AB边上，G在AC边上，EF在斜边BC上，已知AB=3，AC=4，矩形DEFG的面积等于数学公式，则BE的长等于________．

    查看答案和解析>>

    同步练习册答案