
分析 (1)根据积的乘方公式,进行逆运算,即可解答;
(2)转化为同底数幂进行计算,即可解答;
(3)转化为指数相同,再比较底数的大小,即可解答.
解答 解:(1)${5^{2013}}×{(\frac{1}{5})^{2013}}$=$(5×\frac{1}{5})^{2013}$=12013,
故答案为:1.
(2)3×9m×27m=3×(32)m×(33)m=3×32m×33m=31+5m=311,
∴1+5m=11,
解得:m=2.
故答案为:2.
(3)a=255=(25)11=3211,b=344=(34)11=8111,c=533=(53)11=12511,d=622=(62)11=3611,
∵32<36<81<125,
∴3211<3611<8111<12511
∴a<d<b<c,
故答案为:a<d<b<c.
点评 本题考查了幂的乘方和积的乘方,解决本题的关键是公式的逆运用.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 3x2•4x2=12x2 | B. | $\sqrt{2}a+\sqrt{8}a=\sqrt{10}$a | C. | (x5)2=x10 | D. | a10÷a2=a5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
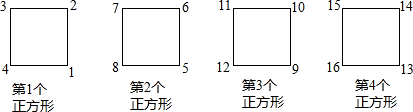
| A. | 第503个正方形的左下角 | B. | 第503个正方形的右下角 | ||
| C. | 第504个正方形的左上角 | D. | 第504个正方形的右下角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{b}$=$\frac{a^2}{b^2}$ | B. | $\frac{a}{b}$=$\frac{ab}{ab}$ | C. | $\frac{a}{b}$=$\frac{a+2c}{b+2c}$(c≠0) | D. | $\frac{a}{b}$=$\frac{ac}{bc}$(c≠0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com