
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C(0,3)
与x轴交于A、B两点,与y轴交于点C(0,3)
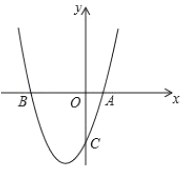
(1)求该抛物线的解析式;
(2)点![]() 为该抛物线上的一点、且在第二象限内,连接
为该抛物线上的一点、且在第二象限内,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若点![]() 为线段
为线段![]() 上一动点,试求
上一动点,试求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)
;(3)![]() .
.
【解析】
(1)把点C(0,3)代入抛物线![]() 即可求出答案;
即可求出答案;
(2)过![]() 点作
点作![]() 轴的垂线,交
轴的垂线,交![]() 轴于点
轴于点![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,利用
,利用![]() 列方程即可求出点
列方程即可求出点![]() 的坐标;
的坐标;
(3)过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() ,可知当
,可知当![]() 、
、![]() 、
、![]() 三点共线时,
三点共线时,![]() 最小,即
最小,即![]() 最小,设直线
最小,设直线![]() 的表达式为:
的表达式为:![]() ,将点
,将点![]() 坐标
坐标![]() 代入求出解析式,并求出
代入求出解析式,并求出![]() 点的坐标,进而可求出
点的坐标,进而可求出![]() 的最小值.
的最小值.
解:(1)把点![]() 的坐标代入抛物线表达式得:
的坐标代入抛物线表达式得:![]() ,
,
解得:![]() ,
,
故该抛物线的解析式为:![]() ;
;
(2)过![]() 点作
点作![]() 轴的垂线,交
轴的垂线,交![]() 轴于点
轴于点![]() ,
,

设:点![]() 的坐标为
的坐标为![]() ,
,
∵![]() ,
,
∴![]() ,
,
即:![]() ,
,![]() ,
,
解得:![]() 或1(舍去
或1(舍去![]() ),
),
故点![]() 的坐标为
的坐标为![]() ;
;
(3)过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,
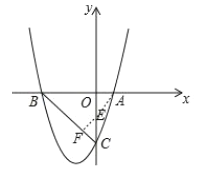
则![]() ,
,![]() ,
,
∴当![]() 、
、![]() 、
、![]() 三点共线时,
三点共线时,![]() 最小,即
最小,即![]() 最小,
最小,
设:直线![]() 的表达式为:
的表达式为:![]() ,
,
将点![]() 坐标
坐标![]() 代入上式,
代入上式,![]() ,则
,则![]() ,
,
则直线![]() 的表达式为:
的表达式为:![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,![]()
![]() .
.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣mx+m﹣2:
(1)求证:不论m为任何实数,此二次函数的图象与x轴都有两个交点;
(2)当二次函数的图象经过点(3,6)时,确定m的值,并写出此二次函数与坐标轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象经过点(x1,0)、(2,0),且﹣2<x1<﹣1,与y轴正半轴的交点在(0,2)的下方,则下列结论:
①abc<0;②b2>4ac;③2a+b+1<0;④2a+c>0.
则其中正确结论的序号是
A. ①② B. ②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(t+1)x2+2(t+2)x+![]() 在x=0和x=2时的函数值相等
在x=0和x=2时的函数值相等
(1)求二次函数的解析式,并作图象;
(2)若一次函数y=kx+6的图象与二次函数的象都经过点A(﹣3,m),求m和k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,王雪带领小朋友玩摸球游戏:在不透明塑料袋里装有1个白色和2个黄色的乒乓球,摸出两个球都是黄色的获胜.小明一次从袋里摸出两个球;小刚左手从袋里摸出一个球,然后右手摸出一个球;小华则先从袋里摸出一个球看一下颜色,又放回袋里,再从袋里摸出一个球.这时,小明急了,说:小刚、小华占了便宜,不公平.你认为如何( ).
A. 不公平,小刚、小华占便宜了 B. 公平 C. 不公平,小华吃亏了 D. 不公平,小华占便宜了
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
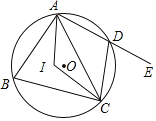
A. 56° B. 62° C. 68° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果把函数y=x2(x≤2)的图象和函数y=![]() 的图象组成一个图象,并称作图象E,那么直线y=3与图象E的交点有_____个;若直线y=m(m为常数)与图象E有三个不同的交点,则常数m的取值范围是_____.
的图象组成一个图象,并称作图象E,那么直线y=3与图象E的交点有_____个;若直线y=m(m为常数)与图象E有三个不同的交点,则常数m的取值范围是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com