
 (x-5)2+5|m|=0;(2)-2a2by+1与3a2b3是同类项.求代数式0.375x2y+5m2x-{-
(x-5)2+5|m|=0;(2)-2a2by+1与3a2b3是同类项.求代数式0.375x2y+5m2x-{-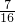 x2y}+[-
x2y}+[- xy2+(-
xy2+(-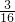 x2y-3.475xy2)-6.2752].
x2y-3.475xy2)-6.2752]. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2015届重庆沙坪坝五校八年级上学期期中联考数学试卷(解析版) 题型:填空题
已知 为等腰三角形的两条边长,且
为等腰三角形的两条边长,且 满足
满足 ,此三角形的周长是_________________.
,此三角形的周长是_________________.
查看答案和解析>>
科目:初中数学 来源:2015届重庆沙坪坝五校八年级上学期期中联考数学试卷(解析版) 题型:填空题
已知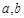 为等腰三角形的两条边长,且
为等腰三角形的两条边长,且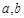 满足
满足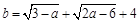 ,此三角形的周长是_________________.
,此三角形的周长是_________________.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(内蒙古赤峰卷)数学 题型:解答题
(2011广西崇左,25,14分)(本小题满分14分)已知抛物线y=x2+4x+m(m为常数)
经过点(0,4).
(1) 求m的值;
(2) 将该抛物线先向右、再向下平移得到另一条抛物线.已知平移后的抛物线满足下述两个条件:它的对称轴(设为直线l2)与平移前的抛物线的对称轴(设为直线l1)关于y轴对称;它所对应的函数的最小值为-8.
① 试求平移后的抛物线的解析式;
② 试问在平移后的抛物线上是否存在点P,使得以3为半径的圆P既与x轴相切,又与直线l2相交?若存在,请求出点P的坐标,并求出直线l2被圆P所截得的弦AB的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(内蒙古乌兰察布卷)数学 题型:解答题
(2011广西崇左,25,14分)(本小题满分14分)已知抛物线y=x2+4x+m(m为常数)
经过点(0,4).
(1) 求m的值;
(2) 将该抛物线先向右、再向下平移得到另一条抛物线.已知平移后的抛物线满足下述两个条件:它的对称轴(设为直线l2)与平移前的抛物线的对称轴(设为直线l1)关于y轴对称;它所对应的函数的最小值为-8.
① 试求平移后的抛物线的解析式;
② 试问在平移后的抛物线上是否存在点P,使得以3为半径的圆P既与x轴相切,又与直线l2相交?若存在,请求出点P的坐标,并求出直线l2被圆P所截得的弦AB的长度;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com