

分析 (1)线段CD的垂直平分线与∠AOB的角平分线的交点即为所求.
(2)分别作点A、B、C关于直线l的对称点A′、B′、C′,连接A′B′、B′C′、A′C′,△A′B′C′即为所求,△ABC的面积利用割补法求解.
(3)作B关于直线AC的对称点B′,连接PB′与AC的交点E即为所求的点E.
解答 解:(1)如图1中,
①作线段CD的垂直平分线MN,
②作∠AOB的角平分线OP,
直线MN与射线OP的交点即为所求的点P.
(2)如图2中,分别作点A、B、C关于直线l的对称点A′、B′、C′,连接A′B′、B′C′、A′C′,△A′B′C′即为所求.
S△ABC=4×4-$\frac{1}{2}$×4×2-$\frac{1}{2}$×2×1-$\frac{1}{2}$×4×3=5.
故答案为5.
(3)如图3中,作B关于直线AC的对称点B′,连接PB′与AC的交点E即为所求的点E.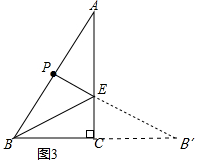
点评 本题考查线段的垂直平分线、角平分线的性质、翻折变换、轴对称变换等知识,解题的关键是熟练掌握这些知识解决问题,属于基础题,中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x$<\frac{3}{2}$ | B. | x$<-\frac{3}{2}$ | C. | x$>\frac{3}{2}$ | D. | x$>-\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
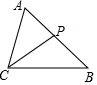 如图,△ABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC和△ACB相似的条件是( )
如图,△ABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC和△ACB相似的条件是( )| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com