
【题目】为提高饮水质量,越来越多的居民选购家用净水器.我市飞龙商场抓住商机,从厂家购进了A、B两种型号家用净水器共100台,A型号家用净水器进价是150元/台,B型号家用净水器进价是250元/台,购进两种型号的家用净水器共用去19000 元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这100台家用净水器的毛利润不低于5600元,求每台A型号家用净水器的售价至少是多少元? (注: 毛利润=售价一进价) .
【答案】(1)A:60台,B:40台;(2)190元
【解析】
(1)可以利用列表分析法对题目进行分析,找出其中的等量关系:
A | B | 总共 | |
购进台数 | x | y | 100 |
进价 | 100 | 250 | |
进货用款 | 100x | 250y | 19000 |
所以可以得到方程组![]()
(2)设每台A型号家用净水器的毛利润是a元,则每台B型号家用浄水器的毛利润是2a元,根据题意得:60a+40×2a![]() 5600。
5600。
解:(1)设A种型号家用净水器购进了x台,B种型号家用净水器购进了y台,
根据题意得![]()
计算得出:![]()
答:A种型号家用浄水器购进了60台,B种型号家用净水器购进了40台;
(2)设每台A型号家用净水器的毛利润是a元,则每台B型号家用浄水器的毛利润是2a元,
根据题意得:60a+40×2a![]() 5600
5600
计算得出:a≥40
∴150+40=190(元)
答:每台A型号家用净水器的售价至少是190元。


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).
(1)求直线AB的解析式及抛物线y=ax2的解析式;
(2)求点C的坐标;
(3)求S△COB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形的是( )
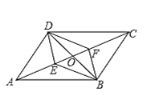
A. AE=CFB. DE=BF
C. ∠ADE=∠CBFD. ∠ABE=∠CDF
查看答案和解析>>
科目:初中数学 来源: 题型:
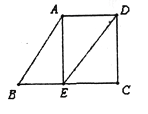
【题目】如图,已知AB∥DE,∠B=60°,AE⊥BC,垂足为点E.
(1)求∠AED的度数;
(2)当∠EDC满足什么条件时,AE∥DC,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
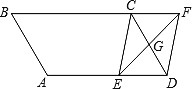
【题目】如图,在平行四边形ABCD中,AB=4cm,BC=6cm,∠B=60°,G是CD的中点,E是边AD上的动点(E不与A、D重合),且点E由A向D运动,速度为1cm/s,EG的延长线与BC的延长线交于点F,连接CE、DF,设点E的运动时间为![]()
(1)求证:无论![]() 为何值,四边形CEDF都是平行四边形;
为何值,四边形CEDF都是平行四边形;
(2)①当![]() s时,CE⊥AD;
s时,CE⊥AD;
②当![]() 时,平行四边形CEDF的两条邻边相等.
时,平行四边形CEDF的两条邻边相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )

A. (1,﹣1) B. (2,0) C. (﹣1,1) D. (﹣1,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() ,
,![]() 分别是直线
分别是直线![]() 上的点.
上的点.
(1)在图1中,判断![]() 和
和![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(2)在图2中,请你直接写出![]() 和
和![]() 之间的数量关系(不需要证明);
之间的数量关系(不需要证明);
(3)在图3中,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
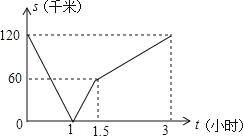
【题目】一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
①A、B两地相距60千米;
②出发1小时,货车与小汽车相遇;
③小汽车的速度是货车速度的2倍;
④出发1.5小时,小汽车比货车多行驶了60千米.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com