
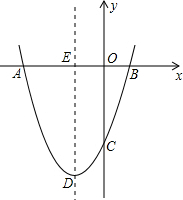
 如图,抛物线y=ax2+bx+c经过点A(-6,0),B(2,0),C(0,-6).
如图,抛物线y=ax2+bx+c经过点A(-6,0),B(2,0),C(0,-6).分析 (1)已知抛物线上的三点坐标,利用待定系数法可求出该二次函数的解析式;
(2)过点P作x轴的垂线,交AC于点N,先运用待定系数法求出直线AC的解析式,设P点坐标为(x,$\frac{1}{2}$x2+2x-6),根据AC的解析式表示出点N的坐标,再根据S△PAC=S△PAN+S△PCN就可以表示出△PAC的面积,运用顶点式就可以求出结论;
(3)分三种情况进行讨论:①以A为直角顶点;②以D为直角顶点;③以M为直角顶点;设点M的坐标为(0,t),根据勾股定理列出方程,求出t的值即可.
解答 解:(1)∵抛物线y=ax2+bx+c经过点A(-6,0),B(2,0),C(0,-6),
∴$\left\{\begin{array}{l}{36a-6b+c=0}\\{4a+2b+c=0}\\{c=-6}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=2}\\{c=-6}\end{array}\right.$.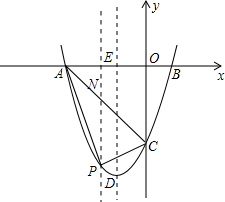 ∴抛物线的解析式为:y=$\frac{1}{2}$x2+2x-6;
∴抛物线的解析式为:y=$\frac{1}{2}$x2+2x-6;
(2)如图,过点P作x轴的垂线,交AC于点N.
设直线AC的解析式为y=kx+m,由题意,得
$\left\{\begin{array}{l}{-6k+m=0}\\{m=-6}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=-6}\end{array}\right.$,
∴直线AC的解析式为:y=-x-6.
设P点坐标为(x,$\frac{1}{2}$x2+2x-6),则点N的坐标为(x,-x-6),
∴PN=PE-NE=-($\frac{1}{2}$x2+2x-6)+(-x-6)=-$\frac{1}{2}$x2-3x.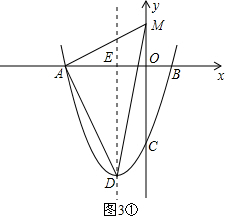 ∵S△PAC=S△PAN+S△PCN,
∵S△PAC=S△PAN+S△PCN,
∴S=$\frac{1}{2}$PN•OA=$\frac{1}{2}$×6(-$\frac{1}{2}$x2-3x)=-$\frac{3}{2}$(x+3)2+$\frac{27}{2}$,
∴当x=-3时,S有最大值$\frac{27}{2}$,此时点P的坐标为(-3,-$\frac{15}{2}$);
(3)在y轴上是存在点M,能够使得△ADM是直角三角形.理由如下:
∵y=$\frac{1}{2}$x2+2x-6=$\frac{1}{2}$(x+2)2-8,
∴顶点D的坐标为(-2,-8),
∵A(-6,0),
∴AD2=(-2+6)2+(-8-0)2=80.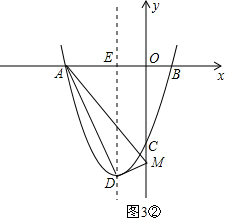 设点M的坐标为(0,t),分三种情况进行讨论:
设点M的坐标为(0,t),分三种情况进行讨论:
①当A为直角顶点时,如图3①,
由勾股定理,得AM2+AD2=DM2,
即(0+6)2+(t-0)2+80=(0+2)2+(t+8)2,
解得t=3,
所以点M的坐标为(0,3);
②当D为直角顶点时,如图3②,
由勾股定理,得DM2+AD2=AM2,
即(0+2)2+(t+8)2+80=(0+6)2+(t-0)2,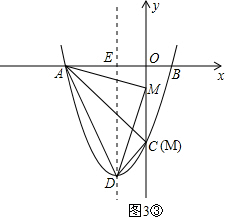 解得t=-7,
解得t=-7,
所以点M的坐标为(0,-7);
③当M为直角顶点时,如图3③,
由勾股定理,得AM2+DM2=AD2,
即(0+6)2+(t-0)2+(0+2)2+(t+8)2=80,
解得t=-2或-6,
所以点M的坐标为(0,-2)或(0,-6);
综上可知,在y轴上存在点M,能够使得△ADM是直角三角形,此时点M的坐标为(0,3)或(0,-7)或(0,-2)或(0,-6).
点评 本题考查的是二次函数综合题,涉及到用待定系数法求一次函数、二次函数的解析式,三角形的面积,二次函数的顶点式的运用,勾股定理等知识,难度适中.运用数形结合、分类讨论及方程思想是解题的关键.


科目:初中数学 来源: 题型:选择题
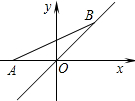 如图,点A的坐标为(-2,0),点B在直线y=x上运动,当线段AB最短时点B的坐标为( )
如图,点A的坐标为(-2,0),点B在直线y=x上运动,当线段AB最短时点B的坐标为( )| A. | (0,0) | B. | (-1,-1) | C. | ($\sqrt{2}$,-$\sqrt{2}$) | D. | (-$\sqrt{2}$,-$\sqrt{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
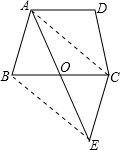 如图,梯形ABCD中,AD∥BC,AB=AD=DC,O是BC中点,将△ABO绕点O旋转180°至△ECO.
如图,梯形ABCD中,AD∥BC,AB=AD=DC,O是BC中点,将△ABO绕点O旋转180°至△ECO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
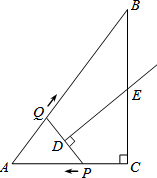 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P,Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P,Q同时出发,当点Q到达点B时停止运动,点P也随之停止运动.设点P,Q运动的时间是t秒(t>0).
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P,Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P,Q同时出发,当点Q到达点B时停止运动,点P也随之停止运动.设点P,Q运动的时间是t秒(t>0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
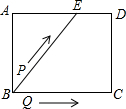 如图,矩形ABCD中,AB=4cm,AD=5cm,点E在AD上,且AE=3cm,点P、Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒,△BPQ的面积为y cm2.则y与t的函数关系图象大致是( )
如图,矩形ABCD中,AB=4cm,AD=5cm,点E在AD上,且AE=3cm,点P、Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒,△BPQ的面积为y cm2.则y与t的函数关系图象大致是( )| A. | 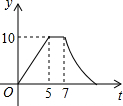 | B. | 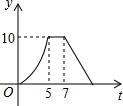 | C. |  | D. | 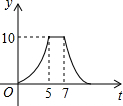 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+3b)(3a-b) | B. | (3a-b)(3a-b) | C. | -(3a-b)(-3a+b) | D. | -(3a-b)(3a+b) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com