练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在△ABC中，点D、E分别在AB、AC边上，BE与CD相交于点F，且AD=AE，∠1=∠2．求证：∠FBC=∠FCB．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017届广东汕头潮阳区九年级上期末模拟数学卷（解析版） 题型：填空题

    若关于x的方程x2+2（k﹣1）x+k2=0有实数根，则k的取值范围是 ．

    查看答案和解析>>

    科目：初中数学 来源：2016届浙江温州市龙湾区中考一模数学试卷（解析版） 题型：解答题

    如图，抛物线y=﹣x2+bx+c与x轴分别交于点A（﹣3，0）和点B，与y轴交于点C（0，3），顶点为点D，对称轴DE交x轴于点E，连接AD，AC，DC．

    （1）求抛物线的函数表达式．

    （2）判断△ADC的形状，并说明理由．

    （3）对称轴DE上是否存在点P，使点P到直线AD的距离与到x轴的距离相等？若存在，求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2016届浙江温州市龙湾区中考一模数学试卷（解析版） 题型：选择题

    若关于x的方程x2﹣2x﹣k=0有两个相等的实数根，则k的值为（ ）

    A．﹣1 B．0 C．﹣3 D．﹣

    查看答案和解析>>

    科目：初中数学 来源：2016届福建泉州晋江市中考二模数学试卷（解析版） 题型：解答题

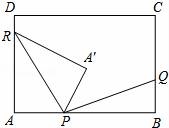
    如图，在矩形ABCD中，AB=8k，BC=5k（k为常数，且k＞0），动点P在AB边上（点P不与A、B重合），点Q、R分别在BC、DA边上，且AP：BQ：DR=3：2：1．点A关于直线PR的对称点为A′，连接PA′、RA′、PQ．

    （1）若k=4，PA=15，则四边形PARA′的形状是 ；

    （2）设DR=x，点B关于直线PQ的对称点为B′点．

    ①记△PRA′的面积为S1，△PQB′的面积为S2．当S1＜S2时，求相应x的取值范围及S2﹣S1的最大值；（用含k的代数式表示）

    ②在点P的运动过程中，判断点B′能否与点A′重合？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2016届福建泉州晋江市中考二模数学试卷（解析版） 题型：填空题

    如图，在?ABCD中，AE⊥BD于点E，∠EAC=30°，AC=12，则AE的长为 ．

    查看答案和解析>>

    科目：初中数学 来源：2016届福建泉州晋江市中考二模数学试卷（解析版） 题型：填空题

    2016的相反数是 ．

    查看答案和解析>>

    科目：初中数学 来源：2017届吉林长春德惠市九年级上期末数学试卷（解析版） 题型：填空题

    如图，已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形，底边BC、CE、EG、GI在同一直线上，且AB=2，BC=1，连接AI，交FG于点Q，则QI= ．

    查看答案和解析>>

    科目：初中数学 来源：2017届湖北鄂州鄂城区九年级上期末数学试卷（解析版） 题型：解答题

    如图，一次函数y=k1x+b（k1≠0）与反比例函数y=（k2≠0）（x＞0）的图象交于A（1，6），B（a，3）两点，

    （1）分别求出一次函数与反比例函数的解析式；

    （2）直接写出k1x+b﹣＞0时x（x＞0）的取值范围；

    （3）如图，等腰梯形OBCD中，BC∥OD，OB=CD，OD边在x轴上，过点C作CE⊥OD于点E，CE和反比例函数图象交于点P，当梯形OBCD的面积为12时，请判断PC和PE的大小关系，并说明理由．

    查看答案和解析>>

    同步练习册答案