
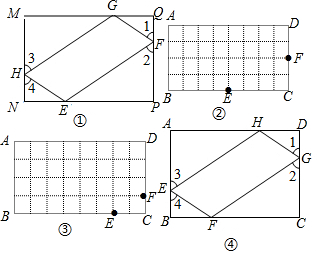
 图①是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图②形状拼成一个正方形.
图①是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图②形状拼成一个正方形.分析 (1)根据拼图的方式即可得出空白部分的正方形的边长;
(2)根据面积公式以及间接法,即可得到图②中空白部分的面积的不同代数式;
(3)根据两种不同的方法表示图②中空白部分的面积相等,即可得到(a+b)2、(a-b)2、ab之间的等量关系;
(4)利用(3)中的等量关系,把a+b=20,ab=70,代入计算即可.
解答 解:(1)空白部分的正方形的边长为a-b;
(2)图②中空白部分的面积=(a-b)2;
图②中空白部分的面积=(a+b)2-4ab;
(3)根据图②可得,(a+b)2-4ab=(a-b)2;
(4)∵(a+b)2-4ab=(a-b)2,a+b=20,ab=70,
∴(a-b)2=202-4×70=120.
点评 本题主要考查了完全平方公式的几何背景,解决问题的关键是运用不同的方式将空白部分的面积表示出来.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
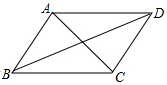 如图,已知四边形ABCD是平行四边形,则下列结论中正确的是( )
如图,已知四边形ABCD是平行四边形,则下列结论中正确的是( )| A. | 当AB⊥BD时,它是矩形 | B. | 当AC=BD时,它是正方形 | ||
| C. | 当∠ABC=90°时,它是菱形 | D. | 当AB=BC时,它是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m+3>n+3 | B. | $\frac{m}{2}$>$\frac{n}{2}$ | C. | -4m>-4n | D. | m-n>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com