
【题目】如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是弧AB上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,点F在线段DE上,且EF=2DF,过点C的直线CG交OA的延长线于点G,且∠CGO=∠CDE. 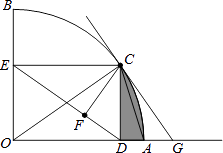
(1)求证:CG与弧AB所在圆相切.
(2)当点C在弧AB上运动时,△CFD的三条边是否存在长度不变的线段?若存在,求出该线段的长度;若不存在,说明理由.
(3)若∠CGD=60°,求图中阴影部分的面积.
【答案】
(1)证明:如图:
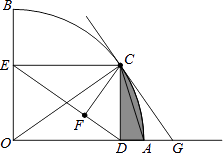 ,
,
∵点C作CD⊥OA于点D,作CE⊥OB于点E,
∴∠CDO=∠CEO=90°,
∵∠DOE=90°,
∴ODCE是矩形,
∴∠CDE+∠EDO=90°,∠EDO=∠COD.
∵∠CGO=∠CDE,
∴∠CGO+COD=90°,
∴∠OCG=90°,
∵CG经过半径OC的外端,
∴CG是⊙O的切线,即CG与弧AB所在圆相切
(2)解:DF不变.
在矩形ODCE中,∵DE=OC=3,EF=2DF,∴DF= ![]() DE=
DE= ![]() OC=1,
OC=1,
DF的长不变,DF=1
(3)解:∵∠CGD=60°,
∴∠COD=30°,
∴CD=OCsin∠COD= ![]() OC=
OC= ![]() ,OD=OCcos∠COD=
,OD=OCcos∠COD= ![]() OC=
OC= ![]() ,
,
图中阴影部分的面积 ![]() ×π×32﹣
×π×32﹣ ![]() CDOD=
CDOD= ![]() ﹣
﹣ ![]()
【解析】(1)根据矩形的判断,可得OCDE的形状,根据矩形的性质,可得∠CDE+∠EDO=90°,∠EDO=∠COD,根据余角的性质,可得∠CGO+COD=90°,根据切线的判定,可得答案;(2)根据矩形的性质,可得CD的长,根据EF与DF的关系,可得DF的长;(3)根据锐角三角函数,可得CD、OD的长,根据根据图形割补法,可得阴影的面积.


科目:初中数学 来源: 题型:
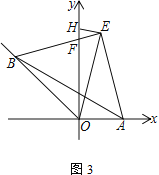
【题目】在平面直角坐标系中,![]() ,点
,点![]() 在第二象限的角平分线上,
在第二象限的角平分线上,![]() 、
、![]() 的垂直平分线交于点
的垂直平分线交于点![]() .
.
(1)求证:![]() ;
;
(2)设![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)作![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,求
,求![]() 点的坐标.
点的坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min{﹣x2+1,﹣x}的最大值是( )
A.![]()
B.![]()
C.1
D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为2的正方形ABCD中,P为AB上一动点,E为AD中点,PE交CD延长线于Q,过E作EF⊥PQ交BC延长线于F,则下列结论:①△APE△DQE;②PQ=EF;③当P为AB中点时,CF= ![]() ;④若H为QC中点,当P从A移动到B时,线段EH扫过的面积为
;④若H为QC中点,当P从A移动到B时,线段EH扫过的面积为 ![]() .其中正确的是( )
.其中正确的是( )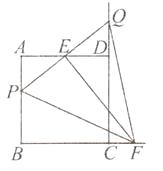
A.①②
B.①②④
C.②③④
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知正方形的边长为a,将此正方形按照下面的方法进行剪拼:第一次,先沿正方形的对边中点连线剪开,然后对接为一个长方形,则此长方形的周长为___;第二次,再沿长方形的对边(长方形的宽)中点连线剪开,对接为新的长方形,如此继续下去,第n次得到的长方形的周长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a-2)![]() +b+3=0,其中a、b为有理数,那么a= ,b= ;
+b+3=0,其中a、b为有理数,那么a= ,b= ;
(2)如果(2+![]() )a-(1-
)a-(1-![]() )b=5,其中a、b为有理数,求a+2b的值.
)b=5,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
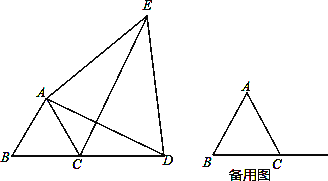
【题目】如图,已知△ABC为等边三角形,点D由点C出发,在BC的延长线上运动,连结AD,以AD为边作等边三角形ADE,连结CE.
(1)请写出AC、CD、CE之间的数量关系,并证明;
(2)若AB=6cm,点D的运动速度为每秒2cm,运动时间为t秒,则t为何值时,CE⊥AD?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com