
【题目】如图,![]() 中
中![]() ,其中
,其中![]() ;
;
(1)求线段![]() 的长(用
的长(用![]() 和
和![]() 的代数式表示);
的代数式表示);
(2)如图1,若![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,点
上,点![]() 到
到![]() 和BC的距离相等,
和BC的距离相等,![]() ,连接
,连接![]() ,求
,求![]() 的长;
的长;
(3)如图2,若![]() 为
为![]() 的中点,
的中点,![]() ,点
,点![]() 分别在线段
分别在线段![]() 上,且
上,且![]() ,连接
,连接![]() ,
,![]() 和
和![]() ,求EF的值;
,求EF的值;

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据勾股定理计算即可;
(2)过F作FM⊥AC于M,FN⊥BC于N,证明四边形FNCM为正方形,利用FN∥AC,得到![]() ,解出正方形的边长,运用勾股定理可求出DF的长;
,解出正方形的边长,运用勾股定理可求出DF的长;
(3)过F作FG⊥AC于点G,根据已知条件证明△ECD≌△DGF,得到条件证明△EDF为等腰直角三角形,再根据等腰直角三角形的性质可求得结果.
解:(1)根据勾股定理,∵BC=a,AC=b,∠ACB=90°,
∴AB=![]() ;
;
(2)由题意可得:BC=6,AC=8,
∴AB=![]() ,
,
过F作FM⊥AC于M,FN⊥BC于N,
∵F到AC和BC距离相等,
可得四边形FNCM为正方形,
设CM=CN=FN=FM=x,
∵FN⊥BC,AC⊥BC,
∴FN∥AC,
∴![]() ,即
,即![]() ,
,
解得:x=![]() ,
,
∴AM=8-x=![]() ,
,
∵AF=AD,
∴AF=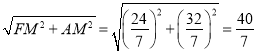 =AD,
=AD,
∴DM=AD-AM=![]() ,
,
∴DF= ;
;

(3)由题意可得:BC=6,AC=8,
∴AB=![]() ,
,
∵F为AB中点,
∴AF=BF=5,
过F作FG⊥AC于点G,
∴FG=![]() BC=3,
BC=3,
∴AG=![]() ,
,
∵BE=BF,AF=AD,
∴BE=5,CE=1,AD=5,CD=3,DG=AD-AG=1,
在△ECD和△DGF中,
 ,
,
∴△ECD≌△DGF(SAS),
∴ED=FD,∠EDC=∠DFG,
∵∠DFG+∠FDG=90°,
∴∠EDC+∠FDG=90°,
∴∠EDF=90°,
∴△EDF为等腰直角三角形,
∵EC=1,CD=3,
∴ED=![]() =FD,
=FD,
∴EF=![]() .
.



 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
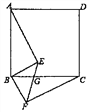
【题目】如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)四边形ABCD中,已知∠ABC+∠ADC=180°,AB=AD,DA⊥AB,点E在CD的延长线上,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)求证:CA平分∠BCD;
(3)如图(2),设AF是△ABC的BC边上的高,求证:EC=2AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在横线上完成下面的证明,并在括号内注明理由.
已知:如图,∠ABC+∠BGD=180°,∠1=∠2.
求证:EF∥DB.
证明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
小明同学遇到下列问题:
解方程组 ,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
令m=2x+3y,n=2x﹣3y,
这时原方程组化为 ,解得
,解得![]() ,
,
把![]() 代入m=2x+3y,n=2x﹣3y.
代入m=2x+3y,n=2x﹣3y.
得![]() 解得
解得![]() .
.
所以,原方程组的解为![]()
(解决问题)
请你参考小明同学的做法,解决下面的问题:
(1)解方程组 ;
;
(2)已知方程组![]() 的解是
的解是![]() ,求方程组
,求方程组![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
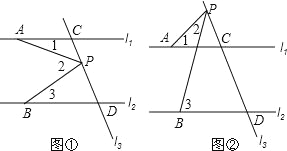
【题目】已知直线 l1∥l2,l3 和 l1,l2 分别交于 C,D 两点,点 A,B 分别在线 l1,l2 上,且位于 l3 的左 侧,点 P 在直线 l3 上,且不和点 C,D 重合.
(1)如图 1,有一动点 P 在线段 CD 之间运动时,试确定∠1、∠2、∠3 之间的关系,并给出证明;
(2)如图 2,当动点 P 在线段 CD 之外运动时,上述的结论是否成立?若不成立,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
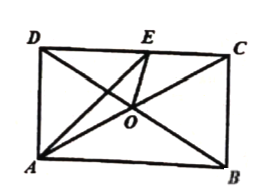
【题目】如图,在矩形![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,给出以下结论:①
,给出以下结论:①![]() 为等腰直角三角形;②
为等腰直角三角形;②![]() 为等边三角形;③
为等边三角形;③![]() ;④
;④![]() ⑤
⑤![]() 是
是![]() 的中位线.其中正确的结论有( )
的中位线.其中正确的结论有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com