
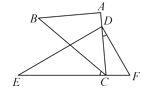
【题目】将一副直角三角板按图11-14摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC,∠E=30°,∠BCE=40°.求∠CDF的度数.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)

查看答案和解析>>
科目:初中数学 来源: 题型:
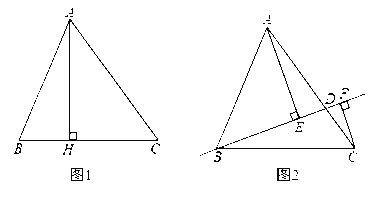
【题目】如图1和2,在△ABC中,AB=13,BC=14,BH=5.
探究:如图1,AH⊥BC于点H,则AH= ,AC= ,△ABC的面积![]() ;
;
拓展:如图2,点D在AC上(可与点A,C重合),分别过点A.C作直线BD的垂线,垂足为E,F,设BD=x,AE=m,CF=n(当点D与点A重合时,我们认为![]() )
)
(1)用含x,m,n的代数式表示![]() 及
及![]() ;
;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,直接写出这样的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 过B(﹣2,6),C(2,2)两点.
过B(﹣2,6),C(2,2)两点.
(1)试求抛物线的解析式;
(2)记抛物线顶点为D,求△BCD的面积;
(3)若直线![]() 向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次课堂练习,小颖同学做了以下几道因式分解题,你认为她做得不够完整的是( )
A.x3-x=x(x2-1)
B.x2y-y3=y(x+y)(x-y)
C.-m2+4n2=(2n+m)(2n-m)
D.3p2-27q2=3(p+3q)(p-3q)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )

A. (a+b)2=a2+2ab+b2 B. (a﹣b)2=a2-2ab+b2
C. (a+b)(a﹣b)= a2﹣b2 D. (a+2b)(a﹣b)=a2+ab﹣2b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列具有相反意义的量是( )
A. 向西走 2 米与向南走 3 米 B. 胜 2 局与负 3 局
C. 增加2厘米和减少2千克 D. 盈利 3 万元与支出 3 万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com