
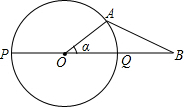
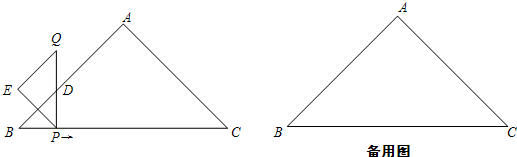
 ��ͼ��PQΪ��O��ֱ������B���߶�PQ���ӳ����ϣ�OQ=QB=1������A�ڡ�O���ϰ�Բ�˶�����P��Q���㣩������AB�����AOB=���������½��ۣ�
��ͼ��PQΪ��O��ֱ������B���߶�PQ���ӳ����ϣ�OQ=QB=1������A�ڡ�O���ϰ�Բ�˶�����P��Q���㣩������AB�����AOB=���������½��ۣ����� ������ͼ1���������������ù��ɶ��������AB��
������ͼ2�����ȿ����ٽ�λ�ã�����A���Q�غ�ʱ���߶�AB��ԲOֻ��һ�������㣬��ʱ��=0�㣻���߶�AB���ڵ�ֱ����ԲO����ʱ���߶�AB��ԲOֻ��һ�������㣬��ʱ��=60�㣮�Ӷ��������ķ�Χ��
�۾���������OAB�ǵ��������Σ���AB=OB����B��BD��AO����OD=$\frac{1}{2}$�����ù��ɶ����ɵ�BD���ó����ۣ�
����AO��PM�Ľ���ΪD������MQ������ͼ3����֤AO��MQ���Ӷ��õ���PDO�ס�PMQ����BMQ�ס�BAO����PO=OQ=BQ���Ӷ��������MQ��OD���������PD��DM��AM��CM��ֵ����AB��
��� �⣺����ͼ1��ʾ��
��AB���O�����ڵ�A��
��OA��AB ��
��
���OAB=90�㣬
��OQ=QB=1��
��OA=1��
��AB=$\sqrt{{OB}^{2}{-OA}^{2}}$=$\sqrt{{2}^{2}{-1}^{2}}$=$\sqrt{3}$��
�ʢ���ȷ��
�ڵ���A���Q�غ�ʱ��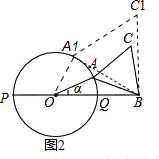
�߶�AB��ԲOֻ��һ�������㣬��ʱ��=0�㣻
���߶�AB���ڵ�ֱ����ԲO����ʱ����ͼ2��ʾ
�߶�A1B��ԲOֻ��һ�������㣬
��ʱOA1��BA1��OA1=1��OB=2��
��cos��A1OB=$\frac{O{A}_{1}}{OB}$=$\frac{1}{2}$��
���A1OB=60�㣬
�൱�߶�AB��ԲOֻ��һ�������㣨��A�㣩ʱ��
���ķ�ΧΪ��0��ܦ���60�㣬
�ʢ���ȷ��
�۹�B��BD��AO����ͼ3��ʾ��
��AB=OB��BD��AO��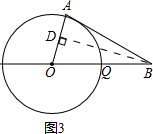
��OD=$\frac{1}{2}$AO=$\frac{1}{2}$��
��BD=$\sqrt{{2}^{2}{-��\frac{1}{2}��}^{2}}$=$\frac{\sqrt{15}}{2}$��
tan�Ϧ�=$\frac{\frac{\sqrt{15}}{2}}{\frac{1}{2}}$=$\sqrt{15}$��
�ʢ۴���
������MQ����ͼ4��ʾ��
��PQ�ǡ�O��ֱ����
���PMQ=90�㣬
��OA��PM��
���PDO=90�㣬
���PDO=��PMQ��
���PDO�ס�PMQ��
��$\frac{PD}{PM}=\frac{DQ}{MQ}=\frac{PO}{PQ}$��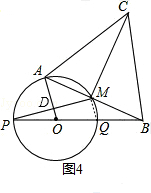
��PO=OQ=PQ��
��PD=PM��OD=MQ��
ͬ����MQ=AO��BM=AB��
��AO=1��
��MQ=$\frac{1}{2}$��
��OD=$\frac{1}{4}$��
�ߡ�PDO=90�㣬PO=1��OD=$\frac{1}{4}$��
��PD=$\frac{\sqrt{15}}{4}$��
��PM=$\frac{\sqrt{15}}{2}$��
��DM=$\frac{\sqrt{15}}{4}$��
�ߡ�ADM=90�㣬AD=A0-OD=$\frac{3}{4}$��
��AM=$\sqrt{{AD}^{2}{+DM}^{2}}$=$\sqrt{{��\frac{3}{4}��}^{2}{+��\frac{\sqrt{15}}{4}��}^{2}}$=$\frac{\sqrt{6}}{2}$��
�ߡ�ABC�ǵȱ������Σ�
��AC=AB=BC����CAB=60�㣬
��BM=AB��
��AM=BM��
��CM��AB��
��AM=$\frac{\sqrt{6}}{2}$��
��BM=$\frac{\sqrt{6}}{2}$��AB=$\sqrt{6}$��
�ʢ���ȷ��
�ʴ�Ϊ���٢ڢܣ�
���� ������Ҫ�����˵ȱ������ε����ʡ����������ε��������ж���ֱ����Բ���С����ɶ������������Ǻ���ֵ��֪ʶ�����������ٽ�ֵ����ǵ�ȡֵ��Χ���������⻭��ͼ�Σ����ν���ǽ�����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{6-2x}{-x+3}$=2 | B�� | $\frac{a-b}{��a-b����a+b��}$=0 | C�� | $\frac{��a-b��^{3}}{��b-a��^{3}}$=1 | D�� | $\frac{��a-b��^{2}}{��b-a��^{2}}$=-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��A1B1C1���ɡ�ABC����ƽ�Ƶõ��ģ����У�A��B��C����Ķ�Ӧ��ֱ���A1��B1��C1��������ƽ��ֱ������ϵ�е��������±���ʾ��
��֪��A1B1C1���ɡ�ABC����ƽ�Ƶõ��ģ����У�A��B��C����Ķ�Ӧ��ֱ���A1��B1��C1��������ƽ��ֱ������ϵ�е��������±���ʾ��| ��ABC | A��a��0�� | B��3��0�� | C��5��5�� |
| ��A1B1C1 | A1��-3��2�� | B1��-1��b�� | C1��c��7�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.151515�� | B�� | �� | C�� | -4 | D�� | $\frac{22}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com