
【题目】若∠AOB=100°,∠BOD=60°,∠AOC=70°时,则∠COD=_____°(自己画图并计算)
【答案】30°或90°或 110°或 130.
【解析】
分四种情况讨论图形的位置,然后根据∠AOB=100°,∠AOC=70°,∠BOD=60°,即可求解.
解:如图①∵∠AOB=100°,∠BOD=60°,∠AOC=70°,
∴∠COD=∠BOC+∠BOD=∠AOB﹣∠AOC+∠BOD=100°﹣70°+60°=90°;
如图②∠COD=360°﹣∠AOB﹣∠BOD﹣∠AOC=360°﹣100°﹣60°﹣70°=130°;
如图③∠COD=∠AOD+∠AOC=∠AOB﹣∠BOD+∠AOC=100°﹣60°+70°=110°;
如图④,∠COD=∠AOC+∠BOD﹣∠AOB=70°+60°﹣100°=30°;
故答案为:30°或90°或 110°或 130.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列方程(1)![]() =2;(2)5x﹣2=2x﹣(3﹣2x);(3)xy=5;(4)
=2;(2)5x﹣2=2x﹣(3﹣2x);(3)xy=5;(4)![]() =﹣2;(5)x2﹣x=1;(6)x=0中一元一次方程有( )
=﹣2;(5)x2﹣x=1;(6)x=0中一元一次方程有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】百货商店销售某种冰箱,每台进价2500元。市场调研表明:当销售价为2900元时,平均每天能售出8台;每台售价每降低10元时,平均每天能多售出1台。(销售利润=销售价—进价)
(1)如果设每台冰箱降价x元,那么每台冰箱的销售利润为 元,平均每天可销售冰箱 台;(用含x的代数式表示)
(2)商店想要使这种冰箱的销售利润平均每天达到5600元,且尽可能地清空冰箱库存,每台冰箱的定价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
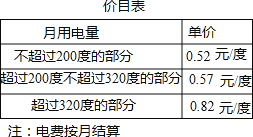
【题目】为了加强公民的节约意识,我市出台阶梯电价计算方案:居民生活用电将月用电量分为三档,第一档为月用电量200度(含)以内,第二档为月用电量200~320度(含),第三档为月用电量320度以上.这三个档次的电价分别为:第一档0.52元/度,第二档0.57元/度,第三档0.82元/度.
若某户居民1月份用电250度,则应收电费:0.52×200+0.57×(250﹣200)=132.5元.
(1)若某户居民10月份电费78元,则该户居民10月份用电_______度;
(2)若该户居民2月份用电340度,则应缴电费_______元;
(3)用x(度)来表示月用电量,请根据x的不同取值范围,用含x的代数式表示出月用电费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图数轴上A、B、C三点对应的数分别是a、b、7,满足OA=3,BC=1,P为数轴上一动点,点P从A出发,沿数轴正方向以每秒1.5个单位长度的速度匀速运动,点Q从点C出发在射线CA上向点A匀速运动,且P、Q两点同时出发.
(1)求a、b的值
(2)当P运动到线段OB的中点时,点Q运动的位置恰好是线段AB靠近点B的三等分点,求点Q的运动速度
(3)当P、Q两点间的距离是6个单位长度时,求OP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结 合.研究数轴我们发现了许多重要的规律:若数轴上点 A、点 B 表示的数分别为 a、b,则A、B 两点之间的距离 AB= ![]() ,线段 AB 的中点表示的数为
,线段 AB 的中点表示的数为![]() .
.
【问题情境】如图,数轴上点A表示的数为-2,点B表示的数为8,点P从点 A 出发, 以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒 2个单 位长度的速度向左匀速运动,设运动时间为t秒(t>0).
【综合运用】(1) 填空:
①A、B两点之间的距离AB=__________,线段AB的中点表示的数为_______;
②用含t的代数式表示:t秒后,点P表示的数为_______;点Q表示的数为_____.
(2) 求当t为何值时,P、Q 两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点 P在运动过程中,线段MN的长度是否发 生变化?若变化,请说明理由;若不变,请求出线段MN的长.
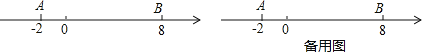
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荆岗中学决定在本校学生中,开展足球、篮球、羽毛球、乒乓球四种活动,为了了解学生对这四种活动的喜爱情况,学校随机调查了该校m名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图. 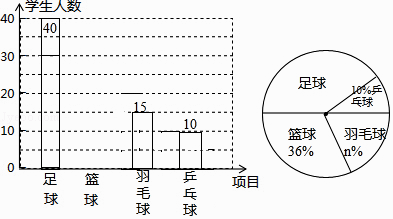
(1)m= , n=;
(2)请补全图中的条形图;
(3)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱踢足球;
(4)在抽查的m名学生中,喜爱乒乓球的有10名同学(其中有4名女生,包括小红、小梅),现将喜爱打乒乓球的同学平均分成两组进行训练,且女生每组分两人,求小红、小梅能分在同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践操作
如图1,在矩形纸片ABCD中,AB>AD.
第一步:如图2,将图1中的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB上的点E处,折痕为AF,再沿EF折叠,然后把纸片展平.
第二步:如图3,将图2中的矩形纸片再次折叠,使点D与点F重合,折痕为GH,然后展平,隐去AF.
第三步:如图4,将图3中的矩形纸片沿AH折叠,得到△AD′H,再沿AD′折叠,折痕为AM,AM与折痕EF交于点N,然后展平.
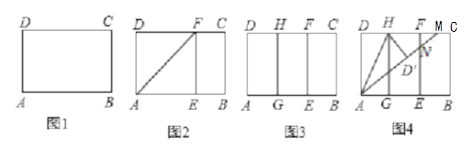
问题解决
(1) 如图2,说明四边形AEFD是正方形;
(2) 如图4,判断NF与ND′的数量关系,并说明理由;
探索发现
(3)图4中MH与AM之间满足MH=nAM,请求出n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家准备给边长为6m的正方形客厅用黑色和白色两种瓷砖铺设,如图所示:①黑色瓷砖区域Ⅰ:位于四个角的边长相同的小正方形及宽度相等的回字型边框(阴影部分),②白色瓷砖区域Ⅱ:四个全等的长方形及客厅中心的正方形(空白部分).设四个角上的小正方形的边长为x(m).

(1)当x=0.8时,若客厅中心的正方形瓷砖铺设的面积为16m2,求回字型黑色边框的宽度;
(2)若客厅中心的正方形边长为4m,白色瓷砖区域Ⅱ的总面积为26m2,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com