
����Ŀ����1����ͼ1�����ı���ABCD�У�AB��AD����BAD��120������B����ADC��90����EF�ֱ��� BC��CD�ϵĵ㣬����EAF��60����̽��ͼ���߶�BE��EF��FD֮���������ϵ��
С��ͬѧ̽��������ķ������ӳ�FD����G��ʹDG��BE������AG����֤����ABE�ա�ADG����֤����AEF�ա�AGF���ɵó����ۣ����Ľ���Ӧ�� ��
̽�����죺
��2����ͼ2�������ı���ABCD�У�AB��AD����B����D��180����E��F�ֱ���BC��CD�ϵĵ㣬����EAF��![]() ��BAD�����������Ƿ���Ȼ��������˵�����ɣ�
��BAD�����������Ƿ���Ȼ��������˵�����ɣ�

���𰸡����ⱳ����BE +DF =EF��̽�����죺������Ȼ���������ɼ�����.
��������
���ⱳ����֤����ABE�ա�ADG���ɵ�AE=AG����֤����AEF�ա�AGF���ɵ�EF=FG�����ɽ��⣻
̽�����죺�ӳ�FD��G��ʹDG=BE������AG������ͬ�ǵIJ�����������B=��ADG��Ȼ���������߽DZ���֤����ABE����ADGȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�AE=AG����BAE=��DAG���������EAF=��GAF��Ȼ���������߽DZ���֤����AEF����GAFȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�EF=GF��Ȼ����⼴�ɣ�
���ⱳ��������ABE����ADG�У�
 ��
��
���ABE�ա�ADG��SAS����
��AE=AG����BAE=��DAG��
�ߡ�EAF=![]() ��BAD��
��BAD��
���GAF=��DAG+��DAF=��BAE+��DAF=��BAD-��EAF=��EAF��
���EAF=��GAF��
����AEF����GAF��
 ��
��
���AEF�ա�AGF��SAS����
��EF=FG��
��FG=DG+DF=BE+DF��
��EF=BE+DF��
�ʴ�Ϊ��EF=BE+DF��
̽�����죺 ������Ȼ�������������£�
��ͼ�ڣ��ӳ�FD��G��ʹDG =BE������AG��

�ߡ�B +��ADC =180�㣬��ADC +��ADG =180�㣬
���B =��ADG��
����ABE����ADG��
 ��
��
���ABE�ա�ADG��SAS����
��AE=AG����BAE=��DAG��
�ߡ�EAF=![]() ��BAD��
��BAD��
���GAF=��DAG+��DAF=��BAE+��DAF=��BAD-��EAF=��EAF��
���EAF=��GAF��
����AEF����GAF��
 ��
��
���AEF�ա�AGF��SAS����
��EF=FG��
��FG=DG+DF=BE+DF��
��EF=BE+DF.


 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д� Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д� ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д� �㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У�AB=AC����BAC=90����ֱ����EPF�Ķ���P��BC�е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F������EPF����ABC���ƶ���P��תʱ����E����A��B�غϣ������������ĸ����ۣ���AE=CF���ڡ�EPF�ǵ���ֱ�������Σ���2S�ı���AEPF=S��ABC����BE+CF=EF������������ʼ����ȷ���У�������

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ƻ�����A��B���ֲ�Ʒ��10�����������ɱ����������±���
A�ֲ�Ʒ | B�ֲ�Ʒ | |
�ɱ�����Ԫ/���� | 2 | 5 |
������Ԫ/���� | 1 | 3 |
��1���������ƻ�����14��Ԫ����A��B���ֲ�ƷӦ�ֱ��������ټ���
��2���������ƻ�Ͷ���ʽ���44��Ԫ���һ�������14��Ԫ�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ӽס����������ѡ����ѡ��һ��ѡ�ֲμ�ʡ���������ֶ����Ƿֱ����5��������ԣ��ɼ��ֱ�Ϊ����λ�������ף�5��6��7��9��8���ң�8��4��8��6��9��
��1�����˶�Ա5������ɼ�����λ��Ϊ________����������________�������˶�Ա����ɼ�������Ϊ________��.
��2����֪��5�γɼ��ķ���Ϊ2��ͨ�����㣬�жϼס��������˶�Ա˭�ijɼ����ȶ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�DZ߳�Ϊ4�������Σ���E�ڱ�AD����ֱ���ϣ�����CE����CEΪ�ߣ���������CEFG��C��E��F��G��˳ʱ�����У�������BF.
��1����ͼ1������E���A�غ�ʱ����ֱ��д��BF�ij���
��2����ͼ2������E���߶�AD��ʱ��AE=1����BF�ij���
��3����BG3![]() ,�������ʱAE�ij�.
,�������ʱAE�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ�� 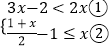 ����������գ���ɱ���Ľ��
����������գ���ɱ���Ľ��
���ⲻ��ʽ�٣�����
���ⲻ��ʽ�ڣ�����
���Ѳ���ʽ�ٺ͢ڵĽ⼯�������ϱ�ʾ������
������ԭ����ʽ��Ľ⼯Ϊ �� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ӵ�����l1��l2�ƽ�У�A��B��l1�ϵ����㣬C��D��l2�ϵ����㣬ij���ڵ�A����á�CAB=90�㣬��DAB=30�㣬����AB����ǰ��20�����E����E���߶�AB�ϣ�����á�DEB=60�㣬��C��D�����ľ��룮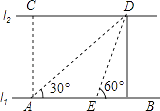
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ȱߡ�ABC�͡�DEF(DE��AB)��ͼ��ʾ�ڷţ���D��BC�ϵ�һ��(��B��C����)���ѡ�DEF�ƶ���D˳ʱ����תһ���ĽǶȣ�ʹ�ñ�DE��DF���ABC�ı�(��BC����)�ֱ��ཻ�ڵ�M��N��
��1����BMD�͡�CDN�����
��2������ʹ��BMD�͡�CDN��ȵ����������ͼ�Σ�
��3���ڣ�2��������ѡһ��ͼ��˵����BMD�͡�CDN��ȵ����ɣ�
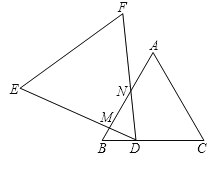
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������͡����������ҡ����������������б�ʾ��������ǵ�ʽ���У���90�㩁���£��ڡ�����90����![]() ������+���£�����
������+���£�����![]() ������������������ȷ���У�������
������������������ȷ���У�������
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com