
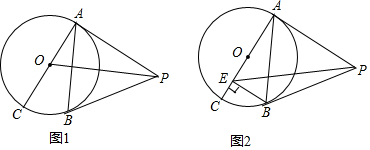
 已知PA,PB与⊙O分别相切于点A,B,AC是⊙O的直径.
已知PA,PB与⊙O分别相切于点A,B,AC是⊙O的直径.分析 (1)如图1中,连接OB.只要证明PA=PB,OA=OB即可解决问题;
(2)如图2中,连接OP交AB于K.首先证明tan∠OPA=tan∠OKA=$\frac{OA}{PA}$=$\frac{1}{2}$,时 OK=a,则AK=BK=2a,PK=4a,PA=2$\sqrt{5}$a,OA=$\sqrt{5}$a,由△OAK∽△BAE,可得$\frac{AK}{AE}$=$\frac{AO}{AB}$,推出AE=$\frac{8}{\sqrt{5}}$a,由BE∥PA,可得∠PEB=∠APE,根据tan∠PEB=tan∠APE,计算即可;
解答 (1)证明:如图1中,连接OB.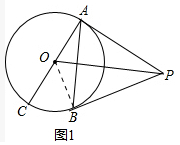
∵PA、PB是⊙O的切线,
∴PA=PB,
∵OA=OB,
∴OP垂直平分线段AB,
即OP⊥AB.
(2)解:如图2中,连接OP交AB于K.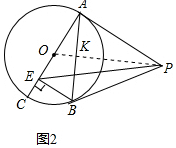
∵PA是⊙O的切线,
∴OA⊥PA,
∴∠PAO=90°,
∵PA=AC=2OA,OP⊥AB,
∴∠OAK+∠AOP=90°,∠AOP+∠APO=90°,
∴∠OAK=∠OPA,
∴tan∠OPA=tan∠OKA=$\frac{OA}{PA}$=$\frac{1}{2}$,时 OK=a,则AK=BK=2a,PK=4a,PA=2$\sqrt{5}$a,OA=$\sqrt{5}$a,
∵△OAK∽△BAE,
∴$\frac{AK}{AE}$=$\frac{AO}{AB}$,
∴AE=$\frac{8}{\sqrt{5}}$a,
∵BE⊥AC,PA⊥AC,
∴BE∥PA,
∴∠PEB=∠APE,
∴tan∠PEB=tan∠APE=$\frac{AE}{AP}$=$\frac{\frac{8}{\sqrt{5}}a}{2\sqrt{5}a}$=$\frac{4}{5}$.
点评 本题考查切线长定理、线段的垂直平分线的性质、锐角三角函数、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,学会利用参数解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
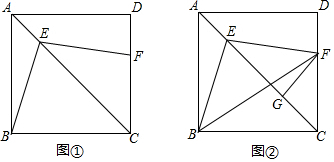
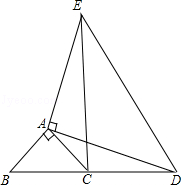 如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.
如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
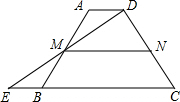 如图,在梯形ABCD中,AD∥BC,延长CB到点E,使BE=AD,连接DE交AB于点M.
如图,在梯形ABCD中,AD∥BC,延长CB到点E,使BE=AD,连接DE交AB于点M.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
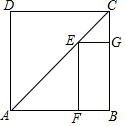 如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,如果正方形ABCD周长为a,那么EF+EG等于$\frac{1}{4}$a.
如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,如果正方形ABCD周长为a,那么EF+EG等于$\frac{1}{4}$a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
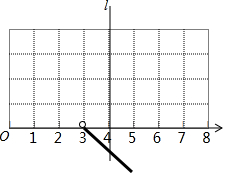 如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示,用坐标描述这个运动,找出小球运动的轨迹上几个关于直线l对称的点,如果小球起始时位于(1,0)处,仍按原来方向击球,请你画出这时小球运动的轨迹.
如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示,用坐标描述这个运动,找出小球运动的轨迹上几个关于直线l对称的点,如果小球起始时位于(1,0)处,仍按原来方向击球,请你画出这时小球运动的轨迹.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com