
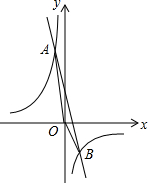
 如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于A(-1,10),B(2,n)两点.
如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于A(-1,10),B(2,n)两点.分析 (1)由点A的坐标,利用待定系数法即可求出k1的值,由点B的横坐标利用反比例函数图象上点的坐标特征可得出点B的坐标,再根据点A、B的坐标利用待定系数法即可求出k2、b的值;
(2)设直线y=-5x+5与x轴交于点C,利用一次函数图象上点的坐标特征求出点C的坐标,利用三角形的面积公式结合S△AOB=S△AOC+S△BOC,即可得出△AOB的面积;
(3)根据两函数图象的上下位置关系,即可得出一次函数值大于反比例函数值的自变量x的取值范围.
解答 解:(1)∵反比例函数y=$\frac{{k}_{1}}{x}$过点A(-1,10),
∴k1=-10,
∵点B(2,n)在反比例函数y=-$\frac{10}{x}$的图象上,
∴n=-$\frac{10}{2}$=-5.
将A(-1,10)、B(2,-5)代入y=k2x+b,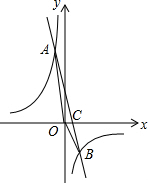
得$\left\{\begin{array}{l}{-{k}_{2}+b=10}\\{2{k}_{2}+b=-5}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{2}=-5}\\{b=5}\end{array}\right.$.
∴k1=-10,k2=-5,b=5.
(2)设直线y=-5x+5与x轴交于点C,
当y=-5x+5=0,x=1,
∴OC=1,
∴S△AOB=S△AOC+S△BOC=$\frac{1}{2}$×1×10+$\frac{1}{2}$×1×5=$\frac{15}{2}$.
(3)观察函数图象,可知:当x<-1或0<x<2时,一次函数图象在反比例函数图象上方,
∴一次函数值大于反比例函数值的自变量x的取值范围为x<-1或0<x<2.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求反比例(一次)函数解析式、反比例(一次)函数图象上点的坐标特征以及三角形的面积,解题的关键是:(1)根据点的坐标,利用待定系数法求出反比例(一次)函数解析式;(2)利用分割图形法求三角形的面积;(3)根据两函数图象的上下位置关系,找出结论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
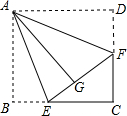 如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.
将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
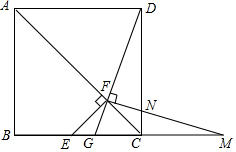 如图.在正方形ABCD中,点E是BC边上的中点,EF⊥AC于点F.连接DF并延长交BC于G.过F作FM⊥DG交CD于N,交BC的延长线于点M.
如图.在正方形ABCD中,点E是BC边上的中点,EF⊥AC于点F.连接DF并延长交BC于G.过F作FM⊥DG交CD于N,交BC的延长线于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 摸球次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
| 出现红色的频数 | 14 | 24 | 38 | 68 | 77 | 92 | 109 | 120 | 132 | |
| 出球红色的频率 | 35% | 32% | 35% | 34% | 33% | 34% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 点P是∠AOB的边OB上一点.
点P是∠AOB的边OB上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com