
ЁОЬтФПЁПНёФъЃЌЮвЙњКЃЙизмЪ№бЯРїДђЛїЁАбѓРЌЛјЁБЮЅЗЈааЖЏЃЌМсОіАбЁАбѓРЌЛјЁБОмгкЙњУХжЎЭтШчЭМЃЌФГЬьЮвЙњвЛЫвКЃМрДЌбВКНЕН![]() ИлПке§ЮїЗНЕФ
ИлПке§ЮїЗНЕФ![]() ДІЪБЃЌЗЂЯждк
ДІЪБЃЌЗЂЯждк![]() ЕФББЦЋЖЋ
ЕФББЦЋЖЋ![]() ЗНЯђЃЌЯрОр
ЗНЯђЃЌЯрОр![]() КЃРяДІЕФ
КЃРяДІЕФ![]() ЕугавЛПЩвЩДЌжЛе§би
ЕугавЛПЩвЩДЌжЛе§би![]() ЗНЯђааЪЛЃЌ
ЗНЯђааЪЛЃЌ![]() Еудк
Еудк![]() ИлПкЕФББЦЋЖЋ
ИлПкЕФББЦЋЖЋ![]() ЗНЯђЩЯЃЌКЃМрДЌЯђ
ЗНЯђЩЯЃЌКЃМрДЌЯђ![]() ИлПкЗЂГіжИСюЃЌжДЗЈДЌСЂМДДг
ИлПкЗЂГіжИСюЃЌжДЗЈДЌСЂМДДг![]() ИлПкби
ИлПкби![]() ЗНЯђЪЛГіЃЌдк
ЗНЯђЪЛГіЃЌдк![]() ДІГЩЙІРЙНиПЩвЩДЌжЛЃЌДЫЪБ
ДІГЩЙІРЙНиПЩвЩДЌжЛЃЌДЫЪБ![]() Еугы
Еугы![]() ЕуЕФОрРыЮЊ
ЕуЕФОрРыЮЊ![]() КЃРяЃЎ
КЃРяЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФЖШЪ§гы
ЕФЖШЪ§гы![]() ЕуЕНжБЯп
ЕуЕНжБЯп![]() ЕФОрРыЃЛ
ЕФОрРыЃЛ
ЃЈ2ЃЉжДЗЈДЌДг![]() ЕН
ЕН![]() КНааСЫЖрЩйКЃРяЃП(НсЙћБЃСєИљКХ)
КНааСЫЖрЩйКЃРяЃП(НсЙћБЃСєИљКХ)
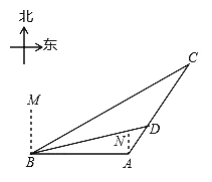
ЁОД№АИЁПЃЈ1ЃЉ30ЁуЃЌ75КЃРяЃЛЃЈ2ЃЉЃЈ75-25![]() ЃЉКЃРяЃЎ
ЃЉКЃРяЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтЕУЁЯC=180Ёу-30Ёу-120Ёу=30ЁуЃЌЙ§ЕуBзїBMЁЭCAНЛCAЕФбгГЄЯпгкЕуMЃЌДгЖјЧѓГіBMЕФжЕЃЌМДПЩЕУЕНД№АИЃЛ
ЃЈ2ЃЉЙ§ЕуDзїDNЁЭBAНЛBAЕФбгГЄЯпгкЕуNЃЌЩшAD=xЃЌдђAN=![]() xЃЌDN=
xЃЌDN=![]() xЃЌИљОнЙДЙЩЖЈРэЃЌСаГіЗНГЬЃЌМДПЩЧѓНтЃЎ
xЃЌИљОнЙДЙЩЖЈРэЃЌСаГіЗНГЬЃЌМДПЩЧѓНтЃЎ
ЃЈ1ЃЉгЩЬтвтЕУЃКЁЯMBC=60ЁуЃЌЁЯABC=30ЁуЃЌЁЯBAC=90Ёу+30Ёу=120ЁуЃЌ
ЁрЁЯC=180Ёу-30Ёу-120Ёу=30ЁуЃЌ
Й§ЕуBзїBMЁЭCAНЛCAЕФбгГЄЯпгкЕуMЃЌ
ЁпBC=150ЃЈКЃРяЃЉЃЌ
ЁрBM=![]() BC=
BC=![]() ЁС150=75ЃЈКЃРяЃЉЃЌ
ЁС150=75ЃЈКЃРяЃЉЃЌ
МДЃК![]() ЕуЕНжБЯп
ЕуЕНжБЯп![]() ЕФОрРыЮЊ75КЃРяЃЛ
ЕФОрРыЮЊ75КЃРяЃЛ
ЃЈ2ЃЉЙ§ЕуDзїDNЁЭBAНЛBAЕФбгГЄЯпгкЕуNЃЌ
ЁпЁЯABC=ЁЯC=30ЁуЃЌ
ЁрAB=BCЁТ![]() =150ЁТ
=150ЁТ![]() =50
=50![]() ЃЈКЃРяЃЉЃЌ
ЃЈКЃРяЃЉЃЌ
ЩшAD=xЃЌ
ЁпЁЯDAN=180Ёу-120Ёу=60ЁуЃЌ
ЁрAN=![]() xЃЌDN=
xЃЌDN=![]() xЃЌ
xЃЌ
ЁпдкRtDBNжаЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌНтЕУЃКx1=75-25
ЃЌНтЕУЃКx1=75-25![]() ЃЌx2=-75-25
ЃЌx2=-75-25![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
Д№ЃКжДЗЈДЌДг![]() ЕН
ЕН![]() КНааСЫЃЈ75-25
КНааСЫЃЈ75-25![]() ЃЉКЃРяЃЎ
ЃЉКЃРяЃЎ




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌBC="3" ЃЌtanЁЯBAC=![]() ЃЌНЋЁЯABCЖделЃЌЪЙЕуCЕФЖдгІЕуHЧЁКУТфдкжБЯпABЩЯЃЌелКлНЛACгкЕуOЃЌвдЕуOЮЊзјБъдЕуЃЌACЫљдкжБЯпЮЊxжсНЈСЂЦНУцжБНЧзјБъЯЕ
ЃЌНЋЁЯABCЖделЃЌЪЙЕуCЕФЖдгІЕуHЧЁКУТфдкжБЯпABЩЯЃЌелКлНЛACгкЕуOЃЌвдЕуOЮЊзјБъдЕуЃЌACЫљдкжБЯпЮЊxжсНЈСЂЦНУцжБНЧзјБъЯЕ
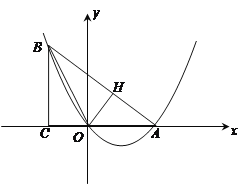
ЃЈ1ЃЉЧѓЙ§AЁЂBЁЂOШ§ЕуЕФХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉШєдкЯпЖЮABЩЯгавЛЖЏЕуPЃЌЙ§PЕузїxжсЕФДЙЯпЃЌНЛХзЮяЯпгкMЃЌЩшPMЕФГЄЖШЕШгкdЃЌЪдЬНОПdгаЮозюДѓжЕЃЌШчЙћгаЃЌЧыЧѓГізюДѓжЕЃЌШчЙћУЛгаЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШєдкХзЮяЯпЩЯгавЛЕуEЃЌдкЖдГЦжсЩЯгавЛЕуFЃЌЧввдOЁЂAЁЂEЁЂFЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃЌЪдЧѓГіЕуEЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМОиаЮЃЌABЃН2BCЃН4ЃЌEЪЧABЖўЕШЗжЕуЃЌжБЯпlЦНаагкжБЯпECЃЌЧвжБЯпlгыжБЯпECжЎМфЕФОрРыЮЊ2ЃЌЕуFдкОиаЮABCDБпЩЯЃЌбижБЯпEFелЕўОиаЮABCDЃЌЪЙЕуAТфдкжБЯпlЩЯЃЌдђDFЃН_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїOABгыЁїOCDЪЧвдЕу0ЮЊЮЛЫЦжааФЕФЮЛЫЦЭМаЮЃЌЯрЫЦБШЮЊ1:2ЃЌЁЯOCD=90![]() ЃЌCO=CD.ШєB(2ЃЌ0)ЃЌдђЕуCЕФзјБъЮЊ( )
ЃЌCO=CD.ШєB(2ЃЌ0)ЃЌдђЕуCЕФзјБъЮЊ( )
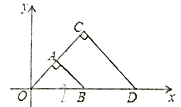
A. (2ЃЌ2) B. (1ЃЌ2) C. ЃЈ![]() ЃЌ2
ЃЌ2![]() ЃЉ D. (2ЃЌ1)
ЃЉ D. (2ЃЌ1)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
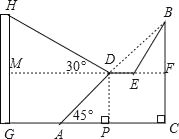
ЁОЬтФПЁПЮЊЕЫаЁЦНЕЎГН110жмФъЯзРёЃЌЙуАВЪаеўИЎЖдГЧЪаНЈЩшНјааСЫећИФЃЌШчЭМЃЌвбжЊаБЦТABГЄ60![]() УзЃЌЦТНЧ(МДЁЯBAC)ЮЊ45ЁуЃЌBCЁЭACЃЌЯжМЦЛЎдкаБЦТжаЕуDДІЭкШЅВПЗжаБЦТЃЌаоНЈвЛИіЦНаагкЫЎЦНЯпCAЕФанЯаЦНЬЈDEКЭвЛЬѕаТЕФаБЦТBE(ЯТУцСНИіаЁЬтНсЙћЖМБЃСєИљКХ)ЃЎ
УзЃЌЦТНЧ(МДЁЯBAC)ЮЊ45ЁуЃЌBCЁЭACЃЌЯжМЦЛЎдкаБЦТжаЕуDДІЭкШЅВПЗжаБЦТЃЌаоНЈвЛИіЦНаагкЫЎЦНЯпCAЕФанЯаЦНЬЈDEКЭвЛЬѕаТЕФаБЦТBE(ЯТУцСНИіаЁЬтНсЙћЖМБЃСєИљКХ)ЃЎ
(1)ШєаоНЈЕФаБЦТBEЕФЦТБШЮЊ![]() ЃК1ЃЌЧѓанЯаЦНЬЈDEЕФГЄЪЧЖрЩйУзЃП
ЃК1ЃЌЧѓанЯаЦНЬЈDEЕФГЄЪЧЖрЩйУзЃП
(2)вЛзљНЈжўЮяGHОрРыAЕу33УздЖ(МДAGЃН33Уз)ЃЌаЁССдкDЕуВтЕУНЈжўЮяЖЅВПHЕФбіНЧ(МДЁЯHDM)ЮЊ30ЁуЃЎЕуBЁЂCЁЂAЁЂGЃЌHдкЭЌвЛИіЦНУцФкЃЌЕуCЁЂAЁЂGдкЭЌвЛЬѕжБЯпЩЯЃЌЧвHGЁЭCGЃЌЮЪНЈжўЮяGHИпЮЊЖрЩйУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуAдкКЏЪ§y=![]() (xЃО0)ЕФЭМЯѓЩЯЃЌЙ§ЕуAзїxжсЁЂyжсЕФДЙЯпЗжБ№НЛКЏЪ§y=
(xЃО0)ЕФЭМЯѓЩЯЃЌЙ§ЕуAзїxжсЁЂyжсЕФДЙЯпЗжБ№НЛКЏЪ§y=![]() (xЃО0ЃЌkЃО2)ЕФЭМЯѓгкЕуBЁЂCЃЌЙ§ЕуCзїxжсЕФДЙЯпНЛy=
(xЃО0ЃЌkЃО2)ЕФЭМЯѓгкЕуBЁЂCЃЌЙ§ЕуCзїxжсЕФДЙЯпНЛy=![]() (xЃО0)ЕФЭМЯѓгкЕуDЃЌСЌНсBCЁЂOCЁЂODЃЎШєЕуAЁЂCЕФКсзјБъЗжБ№ЮЊ1КЭ2ЃЌдђЁїABCгыЁїOCDЕФУцЛ§жЎКЭЮЊ(ЁЁЁЁ)
(xЃО0)ЕФЭМЯѓгкЕуDЃЌСЌНсBCЁЂOCЁЂODЃЎШєЕуAЁЂCЕФКсзјБъЗжБ№ЮЊ1КЭ2ЃЌдђЁїABCгыЁїOCDЕФУцЛ§жЎКЭЮЊ(ЁЁЁЁ)
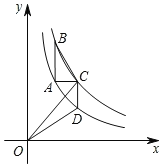
A.2B.3C.4D.6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACB=90ЁуЃЌAB=10ЃЌAC=6ЃЎЖЏЕуPДгЕуAГіЗЂЃЌбиелЯпACЉCBдЫЖЏЃЌдкБпACЩЯвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌдкБпBCЩЯвдУПУы4ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЕНЕуBЭЃжЙЃЌЕБЕуPВЛгыЁїABCЕФЖЅЕужиКЯЪБЃЌЙ§ЕуPзїЦфЫљдкжБНЧБпЕФДЙЯпНЛABгкЕуQЃЛвдQЮЊжБНЧЖЅЕуЯђPQгвВрзїRtЁїPQDЃЌЧвQD=![]() PQЃЎЩшЁїPQDгыЁїABCжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊSЃЌЕуPдЫЖЏЕФЪБМфЮЊt(s)ЃЎ
PQЃЎЩшЁїPQDгыЁїABCжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊSЃЌЕуPдЫЖЏЕФЪБМфЮЊt(s)ЃЎ
ЃЈ1ЃЉЕБЕуPдкБпACЩЯЪБЃЌЧѓPQЕФГЄ(КЌtЕФДњЪ§ЪНБэЪО)ЃЛ
ЃЈ2ЃЉЕуDТфдкБпBCЩЯЪБЃЌЧѓtЕФжЕЃЛ
ЃЈ3ЃЉЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ4ЃЉЩшPDЕФжаЕуЮЊEЃЌзїжБЯпCEЃЎЕБжБЯпCEНЋЁїPQDЕФУцЛ§ЗжГЩ1ЃК5СНВПЗжЪБЃЌжБНгаДГіtЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
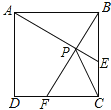
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ2ЕФе§ЗНаЮ![]() жаЃЌЖЏЕу
жаЃЌЖЏЕу![]() ЃЌ
ЃЌ![]() ЗжБ№вдЯрЭЌЕФЫйЖШДг
ЗжБ№вдЯрЭЌЕФЫйЖШДг![]() ЃЌ
ЃЌ![]() СНЕуЭЌЪБГіЗЂЯђ
СНЕуЭЌЪБГіЗЂЯђ![]() КЭ
КЭ![]() дЫЖЏ(ШЮКЮвЛИіЕуЕНДяЭЃжЙ)ЃЌдкдЫЖЏЙ§ГЬжаЃЌдђЯпЖЮ
дЫЖЏ(ШЮКЮвЛИіЕуЕНДяЭЃжЙ)ЃЌдкдЫЖЏЙ§ГЬжаЃЌдђЯпЖЮ![]() ЕФзюаЁжЕЮЊ________ЃЎ
ЕФзюаЁжЕЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЕуOЪЧБпABЩЯвЛЕуЃЌвдЕуOЮЊдВаФЃЌвдOBЮЊАыОЖзїЁбOЃЌЁбOЧЁКУгыACЯрЧагкЕуDЃЌСЌНгBDЃЌBDЦНЗжЁЯABCЃЎ
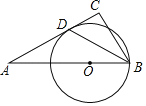
ЃЈ1ЃЉЧѓЁЯCЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШчЙћЁЯAЃН30ЁуЃЌADЃН2![]() ЃЌЧѓЯпЖЮCDЕФГЄЖШЃЎ
ЃЌЧѓЯпЖЮCDЕФГЄЖШЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com