
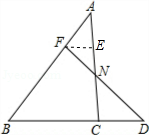
如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,求FN:ND的值.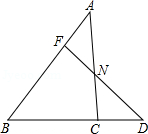
2:3
解析试题分析:过点F作FE∥BD,交AC于点E,求出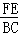 =
= ,得出FE=
,得出FE= BC,根据已知推出CD=
BC,根据已知推出CD= BC,根据平行线分线段成比例定理推出
BC,根据平行线分线段成比例定理推出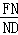 =
=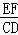 ,代入化简即可.
,代入化简即可.
解:过点F作FE∥BD,交AC于点E,
∴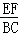 =
= ,
,
∵AF:BF=1:2,
∴ =
= ,
,
∴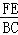 =
= ,
,
即FE= BC,
BC,
∵BC:CD=2:1,
∴CD= BC,
BC,
∵FE∥BD,
∴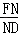 =
=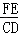 =
= =
=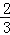 .
.
即FN:ND=2:3.
证法二、连接CF、AD,
∵AF:BF=1:2,BC:CD=2:1,
∴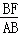 =
=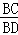 =
=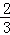 ,
,
∵∠B=∠B,
∴△BCF∽△BDA,
∴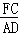 =
=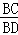 =
=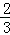 ,∠BCF=∠BDA,
,∠BCF=∠BDA,
∴FC∥AD,
∴△CNF∽△AND,
∴ =
=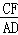 =
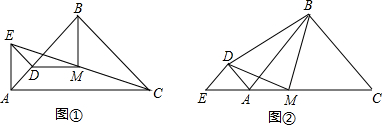
= .
.
考点:平行线分线段成比例.
点评:本题考查了平行线分线段成比例定理的应用,注意:平行线分的线段对应成比例,此题具有一定的代表性,但是一定比较容易出错的题目.


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
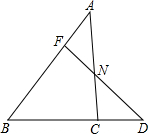 (2012•卢湾区一模)如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,求FN:ND的值.
(2012•卢湾区一模)如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,求FN:ND的值.查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-黄金分割点与平行线分线段成比例(解析版) 题型:解答题
如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,求FN:ND的值.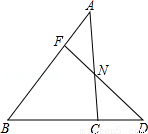
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com