
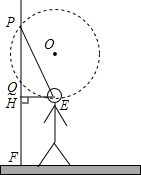
 如图,墙壁上的展品最高点与地面的距离PF=3.2m,最低点与地面的距离QF=2m,观赏者的眼睛E距地面1.6m,经验表明,当水平视线EH与过P、Q、E三点的圆相切于点E时,视角最大,站在此处观赏最理想,求此时点E到墙壁的距离EH.
如图,墙壁上的展品最高点与地面的距离PF=3.2m,最低点与地面的距离QF=2m,观赏者的眼睛E距地面1.6m,经验表明,当水平视线EH与过P、Q、E三点的圆相切于点E时,视角最大,站在此处观赏最理想,求此时点E到墙壁的距离EH. 分析 作OM⊥PQ于M,连结OE,如图,根据垂径定理得到PM=QM=0.6,再计算出QH=QF-HF=0.4,则MH=1,根据切线的性质得OE⊥HE,于是可判断四边形OEHM为矩形,所以OE=MH=1,OM=HE,然后在Rt△POM中,利用勾股定理计算出OM=0.8,从而得到HE=0.8m.
解答 解:作OM⊥PQ于M,连结OE,OP,如图,PM=QM,
∵PF=3.2,QF=2,
∴PQ=1.2,
∴PM=QM=0.6,
∵HF=1.6,
∴QH=QF-HF=0.4,
∴MH=0.4+0.6=1,
∵HE与⊙相切,
∴OE⊥HE,
而HE⊥PF,OM⊥PQ,
∴四边形OEHM为矩形,
∴OE=MH=1,OM=HE,
在Rt△POM中,OP=1,PM=0.6,
∴OM=$\sqrt{{1}^{2}-0.{6}^{2}}$=0.8,
∴HE=0.8m.
答:此时点E到墙壁的距离EH为0.8m.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径;运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查垂径定理和勾股定理.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | -$\frac{5}{3}$ | C. | -$\frac{8}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com