
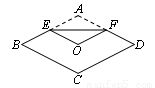
如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若菱形ABCD的边长为2cm,ÐA=120°,则EF= cm.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
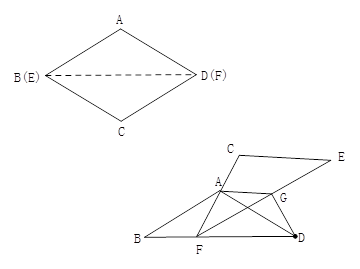
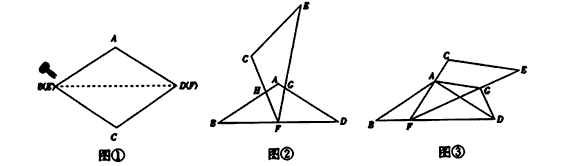
如图①,将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,得到△ABD和△ECF,固定△ABD,并把△ABD与△ECF叠放在一起
(1)操作:如图②,将△ECF的顶点F固定在△ABD的BD边上的中点处,将△ECF绕点F在BD的上方左右旋转,设旋转时FC交BA于H(不与点B重合),EF交DA于G(不与点D重合),求证:BH·GD=BF2
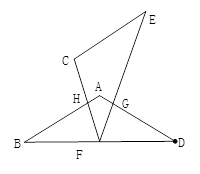 (2)操作:如图③,△ECF的顶点F在△ABD的BD边上滑动(不与点B、D重合),且CF如终过点A,过点A作AG∥CE,交EF于G,连接DG
(2)操作:如图③,△ECF的顶点F在△ABD的BD边上滑动(不与点B、D重合),且CF如终过点A,过点A作AG∥CE,交EF于G,连接DG
探究:FD+DG= ,并请证明你的结论
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2)操作:如图③,△ECF的顶点F在△ABD的BD边上滑动(不与点B、D重合),且CF如终过点A,过点A作AG∥CE,交EF于G,连接DG
(2)操作:如图③,△ECF的顶点F在△ABD的BD边上滑动(不与点B、D重合),且CF如终过点A,过点A作AG∥CE,交EF于G,连接DG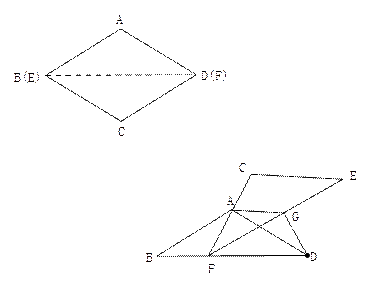
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(湖南岳阳卷)数学 题型:解答题
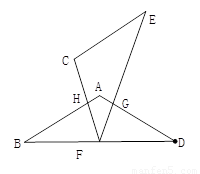
如图①,将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,得到△ABD和△ECF,固定△ABD,并把△ABD与△ECF叠放在一起
(1)操作:如图②,将△ECF的顶点F固定在△ABD的BD边上的中点处,将△ECF绕点F在BD的上方左右旋转,设旋转时FC交BA于H(不与点B重合),EF交DA于G(不与点D重合),求证:BH·GD=BF2
 (2)操作:如图③,△ECF的顶点F在△ABD的BD边上滑动(不与点B、D重合),且CF如终过点A,过点A作AG∥CE,交EF于G,连接DG
(2)操作:如图③,△ECF的顶点F在△ABD的BD边上滑动(不与点B、D重合),且CF如终过点A,过点A作AG∥CE,交EF于G,连接DG
探究:FD+DG= ,并请证明你的结论
 |
查看答案和解析>>
科目:初中数学 来源:湖南省中考真题 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:
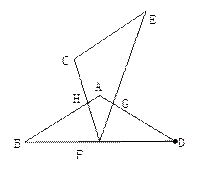
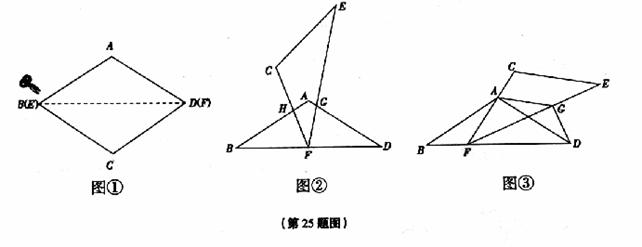
如图①.将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,得到△ABD和△ECF.固定△ABD,并把△ABD与△ECF叠放在—起.
(1)操作:如图②,将△ECF的顶点F固定在△ABD的BD边上的中点处,△ECF绕点F在BD边上方左右旋转,设旋转时FC交BA于点H(H点不与B点重合),FE交DA于点G(G点不与D点重合).
求证:![]()
(2)操作:如图③,△ECF的顶点F在△ABD的BD边上滑动(F点不与B、D点重合),
且CF始终经过点A,过点A作AG∥CE。交FE于点G,连接DG。
探究:![]() _________.请予证明.
_________.请予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com