
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:解答题
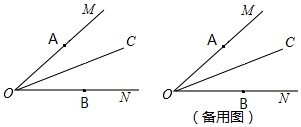
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
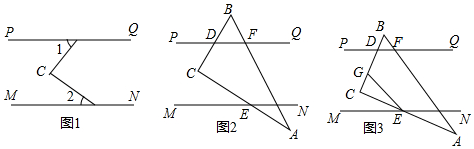
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
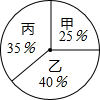 某校学生会决定从三明学生会干事中选拔一名干事当学生会主席,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
某校学生会决定从三明学生会干事中选拔一名干事当学生会主席,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 75 | 80 | 90 |
| 面试 | 93 | 70 | 68 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 无限小数是无理数 | B. | $\sqrt{16}$的平方根是±4 | ||
| C. | -6是(-6)2的一个算术平方根 | D. | -5的立方根是$\root{3}{-5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
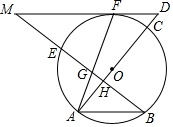 如图,AC是⊙O的直径,弦BE⊥AC于H,F为⊙O上的一点,过F的直线与AC延长线交于点D,与BE的延长线交于点M,连接AF交BM于G,且MF=MG.
如图,AC是⊙O的直径,弦BE⊥AC于H,F为⊙O上的一点,过F的直线与AC延长线交于点D,与BE的延长线交于点M,连接AF交BM于G,且MF=MG.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
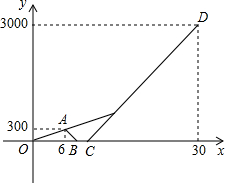 为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6分钟忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前行走,小亮取到借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆.已知单车的速度是步行速度的3倍,如图是小亮和姐姐距家的路程y(米)与出发的时间x(分钟)的函数图象,根据图象解答下列问题:
为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6分钟忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前行走,小亮取到借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆.已知单车的速度是步行速度的3倍,如图是小亮和姐姐距家的路程y(米)与出发的时间x(分钟)的函数图象,根据图象解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com