
 把一张矩形纸片按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=8cm,BC=16cm.
把一张矩形纸片按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=8cm,BC=16cm.分析 (1)由翻折的性质可知:AE=A′E,AB=A′D,∠A=∠A′,然后在△A′ED中,利用勾股定理可求得DE的长,从而可求得△DEF的面积;
(2)过点E作EG⊥BC,在△DFC中,由勾股定理求得FC的长,从而可求得GF的长,最后在△EGF中利用勾股定理求得EF的长即可.
解答 解:(1)由翻折的性质可知:AE=A′E,AB=A′D=8,∠A=∠A′=90°.
设DE=x,则A′E=16-x.
在Rt△A′ED中,由勾股定理得:ED2=A′E2+A′D2,即x2=(16-x)2+82.
解得:x=10.
∴DE=10.
∴△DEF的面积=$\frac{1}{2}ED•AB$=$\frac{1}{2}×10×8$=40cm2.
(2)如图所示,过点E作EG⊥BC.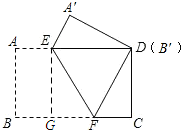
由翻折的性质可知:BF=FD.
设CF=y,则DF=16-y
在Rt△CFD中,由勾股定理得:DF2=FC2+DC2,即(16-y)2=y2+82.
解得:y=6.
∴GF=GC-FC=10-6=4.
在Rt△EFG中,由勾股定理得:EF=$\sqrt{E{G}^{2}+F{G}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$.
点评 本题主要考查的是翻折的性质、勾股定理的应用,掌握翻折的性质是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
 如图,AB=CD=3,∠A=75°,∠B=45°,∠D=15°,则线段AD的长为( )
如图,AB=CD=3,∠A=75°,∠B=45°,∠D=15°,则线段AD的长为( )| A. | 4 | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
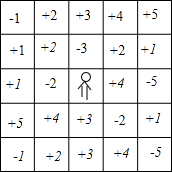 如图是一个“冲出围城”的游戏,规则是:城中人想要冲出围城,可以横走也可以竖走,但不可以斜走,每走一格就可以得到格中相应的分数作为生命值,每格中的分数用乘法累计.当生命值小于+9,并且处于最外圈时,就可以冲出围城,生命值为负数不可以出城.例如:(-2)×(+2)×(+2)×(-1)=+8,就是一条冲出围城的路线.把你找到的冲出围城的路线写下来,也可以直接用箭头将路线在表中表示出来.
如图是一个“冲出围城”的游戏,规则是:城中人想要冲出围城,可以横走也可以竖走,但不可以斜走,每走一格就可以得到格中相应的分数作为生命值,每格中的分数用乘法累计.当生命值小于+9,并且处于最外圈时,就可以冲出围城,生命值为负数不可以出城.例如:(-2)×(+2)×(+2)×(-1)=+8,就是一条冲出围城的路线.把你找到的冲出围城的路线写下来,也可以直接用箭头将路线在表中表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
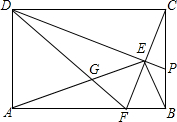 如图所示,在矩形ABCD中.AB=4,BC=3.点F、P分别为线段AB、BC上的动点,CF与DP交于点E,DF与AE交于点G.若GF•DG=AG•GE,连结BE,则BE的最小值为$\sqrt{13}$-2.
如图所示,在矩形ABCD中.AB=4,BC=3.点F、P分别为线段AB、BC上的动点,CF与DP交于点E,DF与AE交于点G.若GF•DG=AG•GE,连结BE,则BE的最小值为$\sqrt{13}$-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com