
| 每回投球次数 | 30 | 60 | 90 | 150 | 200 | 300 | 400 | 500 |
| 每回进球次数 | 27 | 45 | 78 | 118 | 161 | 239 | 322 | 401 |
| 进球频率 | 0.900 | 0.750 | 0.867 | 0.787 | 0.805 | 0.797 | 0.805 | 0.802 |
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:解答题
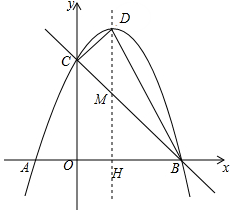 如图,已知抛物线y=-x2+bx+c轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC相交于点M,连接PB.
如图,已知抛物线y=-x2+bx+c轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC相交于点M,连接PB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
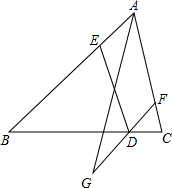 如图,在△ABC中,D,E,F分别为边BC,AB,AC上的点,ED∥AF且ED=AF,延长FD到点G,使DG=FD,求证:ED,AG互相平分.
如图,在△ABC中,D,E,F分别为边BC,AB,AC上的点,ED∥AF且ED=AF,延长FD到点G,使DG=FD,求证:ED,AG互相平分.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
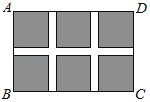 如图,某小区规划在一个长30m,宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,设通道的宽为xm.
如图,某小区规划在一个长30m,宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,设通道的宽为xm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com